Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-10T11:26:31.775Z Has data issue: false hasContentIssue false
  • English
  • Français

K-theory of real algebraic surfaces and threefolds

Published online by Cambridge University Press:  24 October 2008

J. Bochnak  and
W. Kucharz
J. Bochnak
Affiliation:
Department of Mathematics, Vrije Universiteit, P.O. Box 7161, 1007 MC Amsterdam, The Netherlands
W. Kucharz
Affiliation:
Department of Mathematics and Statistics, University of New Mexico, Albuquerque, NM 87131, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be an affine real algebraic variety, i.e., up to biregular isomorphism an algebraic subset of ℝn. (For definitions and notions of real algebraic geometry we refer the reader to the book [6].) Let denote the ring of regular functions on X ([6], chapter 3). (If X is an algebraic subset of ℝn then is comprised of all functions of the form f/g, where g, f: X → ℝ are polynomial functions with g−1(O) = Ø.) In this paper, assuming that X is compact, non-singular, and that dim X ≤ 3, we compute the Grothendieck group 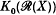of projective modules over (cf. Section 1), and the Grothendieck group and the Witt group of symplectic spaces over (cf. Section 2), in terms of the algebraic cohomology groups and generated by the cohomology classes associated with the algebraic subvarieties of X. We also relate the group 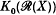to the Grothendieck group KO(X) of continuous real vector bundles over X, and the groups and to the Grothendieck group K(X) of continuous complex vector bundles over X.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 106 , Issue 3 , November 1989 , pp. 471 - 480
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Akbulut, and King, H.. A relative Nash theorem. Trans. Amer. Math. Soc. 267 (1987), 465–481.CrossRefGoogle Scholar
[2]Barge, J. and Ojanguren, M.. Fibrés algébriques sur une surface réelle. Comment. Math. Helv. 62 (1987), 616–629.CrossRefGoogle Scholar
[3]Bass, H.. Algebraic K-theory (Benjamin, 1968).Google Scholar
[4]Bass, H.. Unitary algebraic K-theory. In Algebraic K-Theory III, Lecture Notes in Math. vol. 343 (Springer-Verlag, 1973), pp. 57–267.Google Scholar
[5]Benedetti, R. and Tognoli, A.. Remarks and counterexamples in the theory of real algebraic vector bundles and cycles. In Géométrie Algébrique Réelle et Formes Quadratiques, Lecture Notes in Math. vol. 959 (Springer-Verlag, 1982), pp. 198–211.CrossRefGoogle Scholar
[6]Bochnak, J., Coste, M. and Roy, M.-F.. Géométrie Algébrique Réelle. Ergeb. Math. Grenzgeb. vol. 12 (Springer-Verlag, 1987).Google Scholar
[7]Bochnak, J., Buchner, M. and Kucharz, W.. Vector bundles over real algebraic varieties. (To appear.)Google Scholar
[8]Bochnak, J. and Kucharz, W.. Sur les classes d'homologie représentables par des hypersurfaces algébriques réelles. C. R. Acad. Sci. Paris Sér. I Math. 305 (1987), 609–611.Google Scholar
[9]Bochnak, J. and Kucharz, W.. Algebraic models of smooth manifolds. Invent. Math. (to appear).Google Scholar
[10]Borel, A. and Haefliger, A.. La classe d'homologie fondamentale d'un espace analytique. Bull. Soc. Math. France 89 (1961), 461–513.Google Scholar
[11]Evanss, E. G. Jr. Projective modules as fibre bundles. Proc. Amer. Math. Soc. 27 (1971), 623–626.Google Scholar
[12]Fulton, W.. Intersection Theory. Ergeb. Math. Grenzgeb. vol. 2 (Springer-Verlag, 1984).Google Scholar
[13]Hartshorne, R.. Algebraic Geometry (Springer-Verlag, 1977).Google Scholar
[14]Hirzebruch, F.. Topological Methods in Algebraic Geometry, third edition (Springer-Verlag, 1966).Google Scholar
[15]Husemoller, D.. Fibre Bundles, second edition (Springer-Verlag, 1975).Google Scholar
[16]Kucharz, W.. Vector bundles over real algebraic surfaces and threefolds. Compositio Math. 60 (1986), 209–225.Google Scholar
[17]Kucharz, W.. Topology of real algebraic threefolds. Duke Math. J. 53 (1986), 1073–1079.Google Scholar
[18]Milnor, J. and Husemoller, D.. Symmetric Bilinear Forms. Ergeb. Math. Grenzgeb. vol. 73 (Springer-Verlag, 1973).CrossRefGoogle Scholar
[19]Milnor, J. and Stasheff, J.. Characteristic Classes (Princeton University Press, 1974).CrossRefGoogle Scholar
[20]Ojanguren, M., Parimala, R. and Sridharan, R.. Symplectic bundles over affine varieties. Comment. Math. Helv. 61(1986), 491–500.Google Scholar
[21]Shiota, M.. Real algebraic realizations of characteristic classes. RIMS. Kyoto Univ. 18 (1982), 995–1008.Google Scholar
[22]Spanier, E.. Algebraic Topology (McGraw-Hill, 1966).Google Scholar
[23]Steenrod, N.. The Topology of Fibre Bundles (Princeton University Press, 1951).CrossRefGoogle Scholar
[24]Swan, R.. Vector bundles and projective modules. Trans. Amer. Math. Soc. 105 (1962), 264–277.CrossRefGoogle Scholar
[25]Swan, R.. Topological examples of projective modules. Trans. Amer. Math. Soc. 230 (1977), 201–234.CrossRefGoogle Scholar