Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T18:56:46.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Jordan algebras spanned by Hermitian elements of a Banach algebra

Published online by Cambridge University Press:  24 October 2008

F. F. Bonsall
F. F. Bonsall
Affiliation:
University of Edinburgh
Get access Rights & Permissions [Opens in a new window]

Extract

The Vidav–Palmer theorem [(11), (5), (2) (p. 65)] characterizes C*-algebras among Banach algebras in terms of the algebra and norm structure alone, without reference to an involution, in the following way. Let B denote a complex unital Banach algebra, and let Her (B) denote the set of Hermitian elements of B, that is the elements of B with real numerical ranges. In this notation, the Vidav–Palmer theorem tells us that if

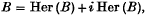
then B is isometrically isomorphic to a C*-algebra of operators on a Hilbert space, with the Hermitian elements corresponding to the self-adjoint operators in the C*-algebra.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 81 , Issue 1 , January 1977 , pp. 3 - 13
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Alfsen, E. M., Shultz, F. W. and størmer, E.A Gelfand–Neumark theorem for Jordan algebras. Preprint, University of Oslo, 1975.Google Scholar
(2)Bonsall, F. F. and Duncan, J.Numerical ranges of operators on normed spaces and of elements of normed algebras. (London Math. Soc. Lecture Note Series 2, Cambridge University Press, 1971).CrossRefGoogle Scholar
(3)Bonsall, F. F.Locally multiplicative wedges in Banach algebras. Proc. London Math. Soc. (3) 30 (1975), 239–256.CrossRefGoogle Scholar
(4)Bonsall, F. F. and Rosenthal, P.Certain Jordan operator algebras and double commutant theorems. J. Functional Analysis 21 (1976), 155–186.CrossRefGoogle Scholar
(5)Palmer, T. W.Characterizations of C*-algebras. Bull. Amer. Math. Soc. 74 (1968), 538–540.CrossRefGoogle Scholar
(6)Power, S. C.C*-modules and an odd–even decomposition for C*-algebras. Bull. London Math. Soc. 8 (1976).CrossRefGoogle Scholar
(7)Rickart, C. E.General theory of Banach algebras (Van Nostrand, 1960; Krieger, 1974).Google Scholar
(8)Sinclair, A. M.The norm of a Hermitian element in a Banach algebra. Proc. Amer. Math. Soc. 28 (1971), 446–450.CrossRefGoogle Scholar
(9)Størmer, E.On the Jordan structure of C*-algebras. Trans. Amer. Math. Soc. 120 (1965), 438–447.Google Scholar
(10)Topping, D.Jordan algebras of self-adjoint operators. Mem. Amer. Math. Soc. 53 (1965), 48 pp.Google Scholar
(11)Vidav, I.Eine metrische Kennzeichnung der selbstadjungierten Operatoren. Math. Zeit. 66 (1956), 121–128.CrossRefGoogle Scholar