Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T20:00:28.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometries of non-commutative Lp-spaces

Published online by Cambridge University Press:  24 October 2008

F. J. Yeadon
F. J. Yeadon
Affiliation:
University of Hull
Get access Rights & Permissions [Opens in a new window]

Extract

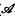The spaces Lp(, φ) for 1 ≤ p ≤ ∞, where φ is a faithful semifinite normal trace on a von Neumann algebra 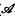, are defined in (10),(2),(14). The problem of determining the general form of an isometry 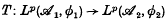of one such space into another has been studied in (i), (6), (9), (12), (5). Our main result, Theorem 2, is a characterization of such isometries for 1 ≤ p ≤ ∞, ≠ 2. The method of proof is based on that of (7), where isometries between Lp function spaces are characterized. The main step in the proof is Theorem 1, which gives the conditions under which equality holds in Clarkson's inequality.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 1 , July 1981 , pp. 41 - 50
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Broise, M. M.Sur les isomorphismes de certaines algèbres de von Neumann. Ann Sci. École Norm. Sup. 83 (1966), 91–111.CrossRefGoogle Scholar
(2)Dixmier, J.Formes linéaires sur un anneau d'opérateurs. Bull. Soc. Math. France 81 (1953), 9–39.Google Scholar
(3)Gleason, A. M.Measures on the closed subspaces of a Hubert space. J. Math. Mech. 6 (1957), 885–894.Google Scholar
(4)Gunson, J.Physical states on quantum logics. Ann. Inst. H. Poincaré 17 (1972), 295–311.Google Scholar
(5)Kadison, R. V.Isometries of operator algebras. Ann. Math. (2) 54 (1951), 325–338.CrossRefGoogle Scholar
(6)Katavolos, A.Isometries of non-commutative Lp-spaces. Canad. J. Math. 28 (1976), 1180–1186.CrossRefGoogle Scholar
(7)Lamperti, J.On the isometries of certain function spaces. Pacific J. Math. 8 (1958), 459–466.CrossRefGoogle Scholar
(8)McCarthy, C. A.cp. Israel J. Math. 5 (1967), 249–271.CrossRefGoogle Scholar
(9)Russo, B.Isometries of Lp-spaces associated with finite von Neumann algebras. Bull. Amer. Math. Soc. 74 (1968), 228–232.CrossRefGoogle Scholar
(10)Segal, I. E.A non-commutative extension of abstract integration. Ann. Math. (2), 57 (1953), 401–457.CrossRefGoogle Scholar
(11)Størmer, E.On the Jordan structure of C*-algebras. Trans. Amer. Math. Soc. 120 (1965), 438–447.Google Scholar
(12)Tam, P. K.Isometries of Lp-spaces associated with semifinite von Neumann algebras. Trans. Amer. Math. Soc. 254 (1979), 339–354.Google Scholar
(13)Tomiyama, J.On the projection of norm one in W*-algebras. Proc. Japan Acad. 33 (1957), 608–612.Google Scholar
(14)Yeadon, F. J.Non-commutative Lp-spaces. Proc. Cambridge Philos. Soc. 77 (1975), 91–102.CrossRefGoogle Scholar