Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T12:34:54.154Z Has data issue: false hasContentIssue false
  • English
  • Français

Isogenies of non-CM elliptic curves with rational j-invariants over number fields

Published online by Cambridge University Press:  01 March 2017

FILIP NAJMAN
FILIP NAJMAN*
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We unconditionally determine 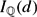$I_{\mathbb Q}(d)$, the set of possible prime degrees of cyclic K-isogenies of elliptic curves with 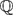${\mathbb Q}$-rational j-invariants and without complex multiplication over number fields K of degree ≤ d, for d ≤ 7, and give an upper bound for 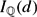$I_{\mathbb Q}(d)$ for d > 7. Assuming Serre's uniformity conjecture, we determine 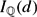$I_{\mathbb Q}(d)$ exactly for all positive integers d.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 1 , January 2018 , pp. 179 - 184
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bilu, Y. and Parent, P. Serre's uniformity problem in the split Cartan case. Ann. Math. (2), 173 (2011), 569–584.Google Scholar
[2] Bilu, Y., Parent, P. and Rebolledo, M. Rational points on X 0 +(p r )( ${\mathbb Q}$ ). Ann. Inst. Fourier (Grenoble) 63 (2013), 957–984.Google Scholar
[3] Cremona, J. Elliptic curve data. Online database https://homepages.warwick.ac.uk/staff/J.E.Cremona/ftp/data/INDEX.html.Google Scholar
[4] Derickx, M., Kamienny, S., Stein, W. and Stoll, M. Torsion points on elliptic curves over number fields of small degree preprint.Google Scholar
[5] Kamienny, S. Torsion points on elliptic curves and q-coefficients of modular forms. Invent. Math. 109 (1992), 221–229.CrossRefGoogle Scholar
[6] Kenku, M. A. The modular curve X 0(39) and rational isogeny. Math. Proc. Camb. Phil. Soc. 85 (1979), 21–23.Google Scholar
[7] Kenku, M. A. The modular curves X 0(65) and X 0(91) and rational isogeny. Math. Proc. Camb. Phil. Soc. 87 (1980), 15–20.Google Scholar
[8] Kenku, M. A. The modular curve X 0(169) and rational isogeny. J. London Math. Soc. (2) 22 (1980), 239–244.Google Scholar
[9] Kenku, M. A. The modular curve X 0(125), X 1(25) and X 1(49). J. London Math. Soc. (2) 23 (1981), 415–427.Google Scholar
[10] Larson, E. and Vaintrob, D. Determinants of subquotients of Galois representations associated with abelian varieties. J. Inst. Math. Jussieu 13 (2014), 517–559.Google Scholar
[11] Lozano–Robledo, Á. On the field of definition of p-torsion points on elliptic curves over the rationals. Math. Ann. 357 (2013), 279–305.Google Scholar
[12] Mazur, B. Modular curves and the Eisenstein ideal. Inst. Hautes Études Sci. Publ. Math. 47 (1978), 33–186.Google Scholar
[13] Mazur, B. Rational isogenies of prime degree. Invent. Math. 44 (1978), pp. 129–162.Google Scholar
[14] Merel, L. Bornes pour la torsion des courbes elliptiques sur les corps de nombres. Invent. Math. 124 (1996), 437–449.Google Scholar
[15] Parent, P. Bornes effectives pour la torsion des courbes elliptiques sur les corps de nombres. J. Reine Angew. Math. 506 (1999), 85–16.Google Scholar
[16] Parent, P. No 17-torsion on elliptic curves over cubic number fields. J. Théor. Nombres de Bordeaux 15 (2003), 831–838.Google Scholar
[17] Serre, J.–P. Propriétés galoisiennes des points d'ordre fini des courbes elliptiques. Invent. Math. 15 (1972), 259–331.Google Scholar
[18] Serre, J.–P. Quelques applications du théoréme de densité de Chebotarev. Publ. Math. IHES 54 (1981), 123–201.Google Scholar
[19] Sutherland, A. Computing images of Galois representations attached to elliptic curves. Forum Math. Sigma 4 (2016), e4.Google Scholar
[20] Zywina, D. On the possible images of the mod l representations associated to elliptic curves over ${\mathbb Q}$ . Preprint, http://www.math.cornell.edu/~zywina/papers/PossibleImages/PossibleImages.pdf.Google Scholar