No CrossRef data available.
Involutory *-antiautomorphisms on On
Published online by Cambridge University Press: 24 October 2008
Extract
Let nℕ{1} and let S1, , Sn be isometries on an infinite-dimensional Hilbert space such that 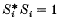 for each i and
for each i and 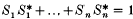 . It was shown in 1 that the C*-algebra On generated by S1, , Sn is an infinite simple C*-algebra which is, up to isomorphism, independent of the choice of isometries satisfying the given relations. Ifis a unital *-endomorphism of On then, as shown in 2,
. It was shown in 1 that the C*-algebra On generated by S1, , Sn is an infinite simple C*-algebra which is, up to isomorphism, independent of the choice of isometries satisfying the given relations. Ifis a unital *-endomorphism of On then, as shown in 2, 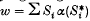 is a unitary determiningby the equations (Si) = w*Si and each unitary arises in this way.
is a unitary determiningby the equations (Si) = w*Si and each unitary arises in this way.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 2 , March 1992 , pp. 319 - 323
- Copyright
- Copyright © Cambridge Philosophical Society 1992
References
REFERENCES
1Cuntz, J.. Simple C*-algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173185.CrossRefGoogle Scholar
2Cuntz, J.. Automorphisms of certain simple C*-algebras. In Quantum. Fields-Algebras Processes (ed. Streit, L.) (Springer-Verlag, 1980), pp. 187196.CrossRefGoogle Scholar
3Cuntz, J.. The structure of addition and multiplication in simple C*-algebras. Math. Scand. 40 (1977), 215233.CrossRefGoogle Scholar
4Cuntz, J.. K-Theory for certain C*-algebras. Ann. of Math. (2) 113 (1981), 181197.CrossRefGoogle Scholar
5Cuntz, J.. K-Theory and C*-algebras. In Proceedings of Conference on K-Theory (Bielefeld, 1982), Lecture Notes in Math. vol. 1046 (Springer-Verlag, 1984), pp. 5579.Google Scholar
9Stacey, P. J.. Stability of involutory *-antiautomorphisms in UHF algebras. J. Operator Theory 24 (1990), 5774.Google Scholar
10Strmer, E.. Conjugacy of involutive antiautomorphisms of von Neumann algebras. J. Fund. Anal. 66 (1986), 5466.CrossRefGoogle Scholar


