Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T21:03:48.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariants of pencils of binary cubics

Published online by Cambridge University Press:  24 October 2008

P. E. Newstead
P. E. Newstead
Affiliation:
University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

Let U denote the variety of pencils of binary cubics without base point defined over an algebraically closed field k whose characteristic is not equal to 2 or 3. (For full details of the terminology, see § 2.) There is a natural action of SL(2) on U; our main object is to show that U possesses a good quotient for this action in the sense of ((7), Definition 1·5) or ((4), p. 70), and to identify this quotient with the affine line 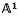over k. In fact, we prove

Theorem 1. There exists a morphism φ: 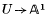such that (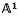, φ) is a good quotient of U by SL(2). Moreover, all but one of the fibres of φ are orbits; the exceptional fibre consists of two orbits corresponding to pencils with one or two triple points.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 2 , March 1981 , pp. 201 - 209
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hartshorne, R.Stable vector bundles of rank 2 on ℙ3. Math. Ann. 238 (1978), 229–280.CrossRefGoogle Scholar
(2)Moore, R. R. Spinors – a semi-classical approach to problems in algebraic geometry. (To appear.)Google Scholar
(3)Mumford, D.Geometric invariant theory (Springer-Verlag, Berlin, Heidelberg, New York, 1965).CrossRefGoogle Scholar
(4)Newstead, P. E.Introduction to moduli problems and orbit spaces (Tata Institute lectures on Mathematics, vol. 51) (Springer-Verlag, Berlin, Heidelberg, New York, 1978).Google Scholar
(5)Salmon, G.Lessons introductory to the modern higher algebra, 3rd edition (Hodges, Foster & Co., Dublin, 1876).Google Scholar
(6)Seshadri, C. S. Mumford's conjecture for GL(2) and applications. In Algebraic Geometry (papers presented at the Bombay colloquium 1968), 347–371 (University Press, Oxford, 1969).Google Scholar
(7)Seshadri, C. S.Quotient spaces modulo reductive algebraic groups. Ann. of Math. 95 (1972), 511–556.CrossRefGoogle Scholar