Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Donkin, Stephen
1992.
Invariants of several matrices.
Inventiones Mathematicae,
Vol. 110,
Issue. 1,
p.
389.
Donkin, Stephen
1994.
Some relative character theory.
Journal of Pure and Applied Algebra,
Vol. 97,
Issue. 3,
p.
281.
Donkin, Stephen
1994.
Finite Dimensional Algebras and Related Topics.
p.
59.
Zubkov, A. N.
1994.
Endomorphisms of tensor products of exterior powers and procesi hypothesis.
Communications in Algebra,
Vol. 22,
Issue. 15,
p.
6385.
Donkin, Stephen
and
Erdmann, Karin
1998.
Tilting Modules, Symmetric Functions, and the Module Structure of the Free Lie Algebra.
Journal of Algebra,
Vol. 203,
Issue. 1,
p.
69.
Jonke, Larisa
and
Meljanac, Stjepan
2002.
Algebra of observables in the Calogero model and in the Chern-Simons matrix model.
Physical Review B,
Vol. 66,
Issue. 20,
Lopatin, A. A.
2004.
The Algebra of Invariants of 3 × 3 Matrices Over a Field of Arbitrary Characteristic.
Communications in Algebra,
Vol. 32,
Issue. 7,
p.
2863.
ZUBKOV, A. N.
2005.
INVARIANTS OF MIXED REPRESENTATIONS OF QUIVERS II: DEFINING RELATIONS AND APPLICATIONS.
Journal of Algebra and Its Applications,
Vol. 04,
Issue. 03,
p.
287.
ZUBKOV, A. N.
2005.
INVARIANTS OF MIXED REPRESENTATIONS OF QUIVERS I.
Journal of Algebra and Its Applications,
Vol. 04,
Issue. 03,
p.
245.
Vaccarino, Francesco
2008.
Generalized symmetric functions and invariants of matrices.
Mathematische Zeitschrift,
Vol. 260,
Issue. 3,
p.
509.
Lopatin, A. A.
2012.
Relations Between O(n)-Invariants of Several Matrices.
Algebras and Representation Theory,
Vol. 15,
Issue. 5,
p.
855.
Lopatin, A.A.
2012.
Free relations for matrix invariants in the modular case.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 2,
p.
427.
Lopatin, Artem A.
2013.
Matrix identities with forms.
Journal of Pure and Applied Algebra,
Vol. 217,
Issue. 11,
p.
2056.
2015.
Computational Aspects of Polynomial Identities.
p.
391.
Ivanyos, Gábor
Qiao, Youming
and
Subrahmanyam, K. V.
2017.
Non-commutative Edmonds’ problem and matrix semi-invariants.
computational complexity,
Vol. 26,
Issue. 3,
p.
717.
Derksen, Harm
and
Makam, Visu
2017.
Polynomial degree bounds for matrix semi-invariants.
Advances in Mathematics,
Vol. 310,
Issue. ,
p.
44.
Derksen, Harm
and
Makam, Visu
2020.
Algorithms for orbit closure separation for invariants and semi-invariants of matrices.
Algebra & Number Theory,
Vol. 14,
Issue. 10,
p.
2791.
DERKSEN, H.
and
MAKAM, V.
2021.
WEYL’S POLARIZATION THEOREM IN POSITIVE CHARACTERISTIC.
Transformation Groups,
Vol. 26,
Issue. 4,
p.
1241.
Zhang, Wenchao
Yavich, Roman
Belov-Kanel, Alexei
Razavinia, Farrokh
Elishev, Andrey
and
Yu, Jietai
2022.
Polynomial Automorphisms, Deformation Quantization and Some Applications on Noncommutative Algebras.
Mathematics,
Vol. 10,
Issue. 22,
p.
4214.
Tange, Rudolf
2025.
Invariants in divided power algebras.
Journal of Algebra,
Vol. 664,
Issue. ,
p.
344.
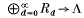 between the graded ring R, whose component Rd in degree d is the character group of the symmetric group of degree d, and the ring of symmetric functions Λ in infinitely many variables (obtained from symmetric functions in n variables by taking the graded inverse limit with respect to n).
between the graded ring R, whose component Rd in degree d is the character group of the symmetric group of degree d, and the ring of symmetric functions Λ in infinitely many variables (obtained from symmetric functions in n variables by taking the graded inverse limit with respect to n).