Published online by Cambridge University Press: 24 October 2008
A recent investigation of the interaction between the Maxwell radiation field and neutral atoms or molecules has led us to consider the relation between the straightforward interaction Hamiltonian
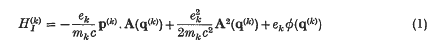
between particle (k) and the radiation field, and the more physical, and explicitly gauge invariant, couplings of the form q. E and µ. H, etc., where q and µ are the electric and magnetic dipole moments of a system of particles. That these latter form of interaction energies follow from well-formulated approximations for atoms in external fields has been known for many years (Goeppert-Mayer(1); see also Rosenfeld(2)). When the Maxwell field is an internal and dynamical field further discussion is necessary, especially concerning the Coulomb interactions. Their advantage has recently been shown in dealing with dipole interactions in the long range Van der Waals force between two neutral systems where the complete coupling, in dipole approximation, is given by — q.ET for each neutral system, where ET is the transverse electric field. The short-range London limit is contained in this coupling despite the absence of longitudinal electric fields (Power and Zienau (3)). In this note we extend these arguments to higher electric multipoles and magnetic multipoles. We also demonstrate their use in the quantum theory of scattering of light, and in particular the derivations of Stephen (4) of the phase angle between emergent beams in optical double refraction phenomena are shown to follow immediately.