Published online by Cambridge University Press: 22 June 2017
Let 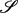 $\mathscr{S}$ be an irreducible topological Markov shift, and let μ be a shift-invariant Gibbs measure on
$\mathscr{S}$ be an irreducible topological Markov shift, and let μ be a shift-invariant Gibbs measure on 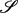 $\mathscr{S}$. Let (Xn)n ≥ 1 be a sequence of i.i.d. random variables with common law μ. In this paper, we focus on the size of the covering of
$\mathscr{S}$. Let (Xn)n ≥ 1 be a sequence of i.i.d. random variables with common law μ. In this paper, we focus on the size of the covering of 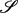 $\mathscr{S}$ by the balls B(Xn, n−s). This generalises the original Dvoretzky problem by considering random coverings of fractal sets by non-homogeneously distributed balls. We compute the almost sure dimension of lim supn →+∞B(Xn, n−s) for every s ≥ 0, which depends on s and the multifractal features of μ. Our results include the inhomogeneous covering of
$\mathscr{S}$ by the balls B(Xn, n−s). This generalises the original Dvoretzky problem by considering random coverings of fractal sets by non-homogeneously distributed balls. We compute the almost sure dimension of lim supn →+∞B(Xn, n−s) for every s ≥ 0, which depends on s and the multifractal features of μ. Our results include the inhomogeneous covering of 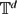 $\mathbb{T}^d$ and Sierpinski carpets.
$\mathbb{T}^d$ and Sierpinski carpets.