Published online by Cambridge University Press: 24 October 2008
If h(r, θ) is harmonic in the unit circle | r | < 1 and satisfies the condition | h | ≤ 1, then there is a function u(ø) which satisfies | u | ≤ 1 such that
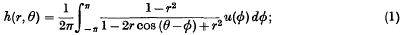
and conversely. Hence, any properties of such harmonic functions should be deducible from equation (1). A number of such properties have been proved by Koebe (Math. Z. 6 (1920), 52–84, 69), using Schwarz's lemma and the geometry of simple conformal transformations. They can be deduced from (1) together with an elementary lemma on the rearrangement of a function (Lemma 1 below). As, however, students of this subject will regard Koebe's method as the one best adapted to establish his theorems, we shall illustrate the alternative method by considering two new problems, namely to find max ∂h/∂r, max ∂h/∂θ, where the maximum in each case is taken for all harmonic functions h which satisfy