Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-02T18:30:48.282Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for permanents and permanental minors

Published online by Cambridge University Press:  24 October 2008

R. A. Brualdi  and
M. Newman
R. A. Brualdi
Affiliation:
National Bureau of Standards, Washington, D.C., U.S.A.
M. Newman
Affiliation:
National Bureau of Standards, Washington, D.C., U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let Ωn denote the convex set of all n × n doubly stochastic matrices: chat is, the set of all n × n matrices with non-negative entries and row and column sums 1. If A = (aij) is an arbitrary n × n matrix, then the permanent of A is the scalar valued function of A defined by

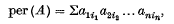
where the subscripts i1, i2, …, in run over all permutations of 1, 2, …, n. The permanent function has been studied extensively of late (see, for example, (1), (2), (3), (4), (6)) and it is known that if A ∈ Ωn then 0 < cn ≤ per (A) ≤ 1, where the constant cn depends only on n. It is natural to inquire if per (A) is a convex function of A for A ∈ Ωn. That this is not the case was shown by a counter-example given by Marcus and quoted by Perfect in her paper ((5)). In this paper, however, she shows that per (½I + ½A) ≤ ½ + ½ per (A) for all A ∈ Ωn. Here I = In is the identity matrix of order n.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 61 , Issue 3 , July 1965 , pp. 741 - 746
Copyright
Copyright © Cambridge Philosophical Society 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Marcus, H. and Minc, H.A survey of matrix theory and matrix inequalities (Allyn and Bacon; Boston, 1964).Google Scholar
(2)Marcus, M. and Newman, M.Inequalities for the permanent function. Ann. of Math. 75 (1962), 47–62.CrossRefGoogle Scholar
(3)Marcus, M. and Newman, M.On the minimum of the permanent of a doubly stochastic matrix. Duke Math. J. 26 (1959), 61–72.Google Scholar
(4)Marcus, M. and Gordon, W. R.Inequalities for subpermanents. Illinois J. Math. 8 (1964), 607–614.Google Scholar
(5)Perfect, H.An inequality for the permanent function. Proc. Cambridge Philos. Soc. 60 (1964), 1030–1031.Google Scholar
(6)Ryser, H. J.Combinatorial mathematics. Garus Math. Monograph, no. 14 (Wiley; New York, 1963).CrossRefGoogle Scholar