Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T08:51:53.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Increasing subsequences of random walks

Published online by Cambridge University Press:  23 September 2016

OMER ANGEL ,
RICHÁRD BALKA  and
YUVAL PERES
OMER ANGEL
Affiliation:
University of British Columbia, Vancouver BC, V6T 1Z2, Canada. e-mail: [email protected]
RICHÁRD BALKA
Affiliation:
University of British Columbia, and Pacific Institute for the Mathematical Sciences, Vancouver BC, V6T 1Z2, Canada. e-mail: [email protected]
YUVAL PERES
Affiliation:
Microsoft Research, 1 Microsoft Way, Redmond, WA 98052, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a sequence of n real numbers {Si}i⩽n, we consider the longest weakly increasing subsequence, namely i1 < i2 < . . . < iL with Sik ⩽ Sik+1 and L maximal. When the elements Si are i.i.d. uniform random variables, Vershik and Kerov, and Logan and Shepp proved that 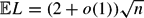${\mathbb E} L=(2+o(1)) \sqrt{n}$.

We consider the case when {Si}i⩽n is a random walk on ℝ with increments of mean zero and finite (positive) variance. In this case, it is well known (e.g., using record times) that the length of the longest increasing subsequence satisfies ${\mathbb E} L\geq c\sqrt{n}$. Our main result is an upper bound ${\mathbb E} L\leq n^{1/2 + o(1)}$, establishing the leading asymptotic behavior. If {Si}i⩽n is a simple random walk on ℤ, we improve the lower bound by showing that 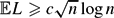${\mathbb E} L \geq c\sqrt{n} \log{n}$.

We also show that if {Si} is a simple random walk in ℤ2, then there is a subsequence of {Si}i⩽n of expected length at least cn1/3 that is increasing in each coordinate. The above one-dimensional result yields an upper bound of n1/2+o(1). The problem of determining the correct exponent remains open.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 163 , Issue 1 , July 2017 , pp. 173 - 185
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Angel, O., Balka, R., Máthé, A. and Peres, Y. Restrictions of Hölder continuous functions, submitted, arXiv:1504.04789.Google Scholar
[2] Baik, J., Deift, P. and Johansson, K. On the distribution of the length of the longest increasing subsequence of random permutations. J. Amer. Math. Soc. 12 (1999), 1119–1178.Google Scholar
[3] Balka, R. and Peres, Y. Restrictions of Brownian motion. C. R. Math. Acad. Sci. Paris 352 (2014), no. 12, 1057–1061.CrossRefGoogle Scholar
[4] Denisov, D. and Wachtel, V. Random walks in cones. Ann. Probab. 43 (2015), no. 3, 992–1044.Google Scholar
[5] Elekes, M. Hausdorff measures of different dimensions are isomorphic under the Continuum Hypothesis. Real Anal. Exchange 30 (2004), no. 2, 605–616.CrossRefGoogle Scholar
[6] Erdős, P. and Szekeres, G. A combinatorial problem in geometry. Composition Math. 2 (1935), 463–470.Google Scholar
[7] Kahane, J.-P. and Katznelson, Y. Restrictions of continuous functions. Israel J. Math. 174 (2009), 269–284.CrossRefGoogle Scholar
[8] Lawler, G. F. and Limic, V. Random walk: A modern introduction (Cambridge University Press, 2010).Google Scholar
[9] Levin, D. A., Peres, Y. and Wilmer, E. L. Markov chains and mixing times, with an Appendix written by Propp, J. G. and Wilson, D. B. (American Mathematical Society, 2009).Google Scholar
[10] Logan, B. F. and Shepp, L. A. A variational problem for random Young tableaux. Adv. Math. 26 (1977), 206–222.CrossRefGoogle Scholar
[11] Máthé, A. Measurable functions are of bounded variation on a set of Hausdorff dimension 1/2. Bull. London Math. Soc. 45 (2013), 580–594.Google Scholar
[12] Romik, D. The Surprising Mathematics of Longest Increasing Subsequences (Cambridge University Press, New York, 2015).CrossRefGoogle Scholar
[13] Petrov, V. V. On an estimate of the concentration function of a sum of independent random variables. Teor. Veroyatnost. Primen. 15 (1970), no. 4, 718–721. English translation in Theor. Probab. Appl. 15 (1970), no. 4, 701–703.Google Scholar
[14] Ulam, S. M. Monte Carlo calculations in problems of mathematical physics. Modern Mathematics for the Engineer. Second series, edited by Beckenbach, E. F. (McGraw-Hill, 1961), 261–281.Google Scholar
[15] Vershik, A. M. and Kerov, S. V. Asymptotic behavior of the Plancherel measure of the symmetric group and the limit form of Young tableaux (Russian). Dokl. Akad. Nauk SSSR 223 (1977), 1024–1027. English translation in Soviet Math. Dokl. 233 (1977), 527–531.Google Scholar