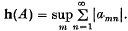Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T07:28:53.398Z Has data issue: false hasContentIssue false
  • English
  • Français

Inclusion of sets of regular summability matrices. II

Published online by Cambridge University Press:  24 October 2008

J. W. Baker  and
G. M. Petersen
J. W. Baker
Affiliation:
University College, Swansea
G. M. Petersen
Affiliation:
University College, Swansea
Get access Rights & Permissions [Opens in a new window]

Extract

1. In a previous paper, ((1)), we have discussed problems which arise in finding a matrix which is in some sense stronger than each of a set of regular summability matrices. We intend in this paper to clear up other problems in this subject. We shall retain the notation and definitions of (1) throughout, but shall later modify one set of definitions in the light of some of our results. In this paper, the term matrix will be reserved for regular summability matrices. Also, u will be used to denote the unit sequence, u = {un} = {1} and h(A) will be used to denote the norm of the matrix A = (amn), i.e.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 61 , Issue 2 , April 1965 , pp. 381 - 394
Copyright
Copyright © Cambridge Philosophical Society 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, J. W. and Petersen, G. M.Inclusion of sets of regular summability matrices. Proc. Cambridge Philos. Soc. 60 (1964), 705–712.CrossRefGoogle Scholar
(2)Brudno, A. L.Summation of bounded sequences. Mat. Sb. 16 (1954), 191–247 (in Russian).Google Scholar
(3)Brudno, A. L.Relative norms of Toeplitz matrices. Dokl. Akad. Nauk S.S.S.R. 91 (1953), 197–200 (in Russian).Google Scholar
(4)Lorentz, G. G. and Zeller, K.. Über paare von Limitierungsverfahren. Math. Z. 68 (1958), 428–438.CrossRefGoogle Scholar
(5)Petersen, G. M.Summability and bounded sequences. Proc. Cambridge Philos. Soc. 55 (1959), 257–261.CrossRefGoogle Scholar
(6)Petersen, G. M.On pairs of summability matrices. Quart. J. Math. Oxford Ser. (to appear).Google Scholar
(7)Petersen, G. M.Consistency of summation matrices for unbounded sequences. Quart. J. Math. Oxford Ser. 14 (1963), 161–169.CrossRefGoogle Scholar