Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T11:25:17.595Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperspaces of a uniformizable space

Published online by Cambridge University Press:  24 October 2008

D. Hammond Smith
D. Hammond Smith
Affiliation:
University of Exeter
Get access Rights & Permissions [Opens in a new window]

Extract

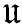If X is a uniformizable space any uniform structure compatible with its topology will give a uniform structure 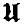on the collection H(X) of all non-empty closed sets of X ((1), Section 2, Exercises 7, 8, definition 1·6): for each entourage U ∈ 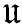we define an entourage U on H(X) by putting U = {(A, B); A ⊂ U(B) and B ⊂ U(A)}. It has been conjectured ((6), p. 35, Exercise 17) that if 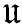1 and 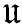2 are distinct uniform structures on X, 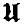1 and 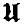2 induce indifferent topologies on H(X). Unfortunately the method proposed in (6) fails, even for metrizable structures, as we shall show by an example. We shall, however, establish a number of partial results tending to support the conjecture; in particular we shall establish the result when both the uniform structures are metrizable, or when one is precompact.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 25 - 28
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Bourbaki, N.Topologie générale, Ch. II (Paris; Hermann, 1940).Google Scholar
(2)Bourbaki, N.Topologie générale, Ch. III (Paris; Hermann, 1942).Google Scholar
(3)Efremovich, V. A.Proximity spaces. Dokl. Akad. Nauk SSSR 76 (1951), 341–343.Google Scholar
(4)Gál, I. S.Proximity relations and precompact structures. (Nederl. Akad. Wetensch. Indag. Math.), 21 (1959), 304–326.CrossRefGoogle Scholar
(5)Hausdorff, F.Mengenlehre, 3rd Revised Edition (New York; Dover).Google Scholar
(6)Isbell, J. R.Uniform spaces. Providence, Rhode Island (American Math. Soc., 1964).CrossRefGoogle Scholar
(7)Michael, E.Topologies on spaces of subsets. Trans. American Math. Soc. 71 (1951), 152–182.Google Scholar
(8)Pervin, W. J.Foundations of general topology (New York; Academic Press, 1964).Google Scholar