Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T13:33:48.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Hurewicz test sets for generalized separation and reduction

Published online by Cambridge University Press:  01 September 2007

TAMÁS MÁTRAI
TAMÁS MÁTRAI*
Affiliation:
Department of Mathematics and its Applications, Central European University, Nádor u. 6. 1051, Budapest, Hungary. email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a Hurewicz-type theorem for generalized separation: we present a method which allows us to test if for a sequence of Borel sets (Ai)i > ω satisfying 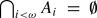there is a sequence (Bi)i < ω of Π0ξ sets such that 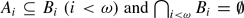or not. We also prove an analogous result for generalized reduction. The results of the paper are motivated by a Hurewicz-type theorem of A. Louveau and J. Saint Raymond on ordinary separation of analytic sets.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 143 , Issue 2 , September 2007 , pp. 407 - 417
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Debs, G. and Raymond, J. Saint. Effective refining of Borel coverings. Preprint.Google Scholar
[2]Kechris, A. S.. Classical Descriptive Set Theory. Graduate Texts in Mathematics 156 (Springer-Verlag, 1994).Google Scholar
[3]Louveau, A. and Raymond, J. Saint. Borel Classes and Closed Games: Wadge-type and Hurewicz-type Results. Trans. Amer. Math. Soc., 304, No. 2 (1987) 431–467.Google Scholar
[4]Mátrai, T.. Hurewicz tests: separating and reducing analytic sets the conscious way. PhD Thesis (Central European University, 2005).Google Scholar
[5]Mátrai, T.. On the closure of Baire classes under transfinite convergences. Fund. Math. 183 (2004), 157–168.Google Scholar
[6]Moschovakis, Y.. Descriptive Set Theory. Studies in Logic and the Foundations of Mathematics, Volume 100 (North-Holland Publishing Co., 1980).Google Scholar