Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T12:41:01.827Z Has data issue: false hasContentIssue false
  • English
  • Français

Hopf algebras and regular isotopy invariants for link diagrams

Published online by Cambridge University Press:  24 October 2008

M. A. Hennings
M. A. Hennings
Affiliation:
Sidney Sussex College, Cambridge CB2 3HU
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, we shall consider the following method for obtaining regular isotopy invariants of link diagrams. Given any link diagram L, equip it with a Morse function h, so that the diagram consists entirely of crossings, maxima, minima and vertical arcs. Introduce 2-valent graphical vertices to separate the various segments of the diagram. Given a finite index set I, a state σ for Lh is an assignation of one element of I to each graphical vertex. Each segment of the diagram now has a weight

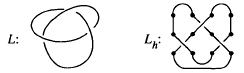
associated with it, given in terms of tensor coordinates indexed by the set I by the pictures

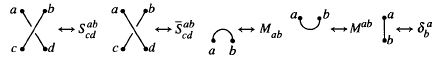
and, for any state σ, [Li|σ] denotes the product of the various weights. We then define 〈Lh〉 to be the sum of [Lh|σ] over all possible states σ,

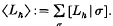
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 1 , January 1991 , pp. 59 - 77
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Kauffman, L. H.. Knots, abstract tensors and the Yang–Baxter equation. (IHES Preprint IHES/M/89/24, 1989.)Google Scholar
[2]Kirillov, A. N. and Reshetikhin, N. Yu. Representation of the algebra Uqsl (2), q-orthogonal polynomials and invariants of links. (LOMI Preprint E-9–88, 1988.)Google Scholar
[3]Larson, R. G. and Radford, D. E.. Finite-dimensional cosemisimple Hopf algebras in characteristic zero are semisimple. J. Algebra 117 (1988), 267–289.CrossRefGoogle Scholar
[4]Labson, R. G. and Radford, D. E.. Semisimple cosemisimple Hopf algebras. Amer. J. Math. 110 (1988), 187–195.Google Scholar
[5]Larson, R. G. and Sweedler, M. E.. An associative orthogonal bilinear form for Hopf algebras. Amer. J. Math. 91 (1969), 75–94.CrossRefGoogle Scholar
[6]Majid, S.. Quasitriangular Hopf algebras and Yang–Baxter equations. (Preprint, 1989.)CrossRefGoogle Scholar
[7]Pierce, R. S.. Associative Algebras. Graduate Texts in Math. no. 88 (Springer-Verlag, 1982).CrossRefGoogle Scholar
[8]Reshetikhin, N. Yu and Turaev, V. G.. Ribbon graphs and their invariants derived from quantum groups. (MSRI Preprint 03508–89, 1989.)Google Scholar
[9]Vogel, P.. Representations of links by braids – a new algorithm. (Preprint, 1989.)Google Scholar