Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T01:29:23.369Z Has data issue: false hasContentIssue false
  • English
  • Français

Homomorphs and wreath product extensions

Published online by Cambridge University Press:  24 October 2008

Peter Förster
Peter Förster
Affiliation:
University of Mainz, Germany
Get access Rights & Permissions [Opens in a new window]

Extract

A homomorph is a class of (finite soluble) groups closed under the operation Q of taking epimorphic images. (All groups considered in this paper are finite and soluble.) Among those types of homomorphs that have found particular interest in the theory of finite soluble groups are formations and Schunck classes; the reader is referred to (2), § 2, for a definition of those classes. In the present paper we are interested in homomorphs 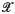satisfying the following additional closure property:

(W0) if A is abelian with elementary Sylow subgroups, then each wreath product A 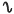G (with respect to an arbitrary permutation representation of G) with G ∊ 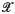is contained in .

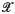Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 92 , Issue 1 , July 1982 , pp. 93 - 99
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Doerk, K.Zwei Klassen von Formationen endlieher auflösbarer Gruppen, deren Halbver-band gesättigfcer Unterformationen genau ein maximales Element besitzt. Arch. Math. 21 (1970), 240–244.CrossRefGoogle Scholar
(2)Förster, P.Charakterisierungen einiger Schunckklassen endlieher auflösbarer Gruppen I. J. Algebra 55 (1978), 155–187.CrossRefGoogle Scholar
(3)Förster, P.Closure operations for Schunck classes and formations of finite solvable groups. Math. Proc. Cambridge Phil. Soc. 85 (1979), 253–259.CrossRefGoogle Scholar
(4)Förster, P.Über die iterierten Definitionsbereiche von Homomorphen endlicher auflösbarer Gruppen. Arch. Math. 35 (1980), 27–41.CrossRefGoogle Scholar
(5)Förster, P.Prefrattini Groups. J. Austral. Math. Soc. (in the Press).Google Scholar
(6)Huppert, B.Endliche Gruppen I (Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar