Article contents
A heat trace anomaly on polygons
Published online by Cambridge University Press: 19 June 2015
Abstract
Let Ω0 be a polygon in 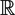 $\mathbb{R}$2, or more generally a compact surface with piecewise smooth boundary and corners. Suppose that Ωε is a family of surfaces with
$\mathbb{R}$2, or more generally a compact surface with piecewise smooth boundary and corners. Suppose that Ωε is a family of surfaces with 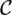 ${\mathcal C}$∞ boundary which converges to Ω0 smoothly away from the corners, and in a precise way at the vertices to be described in the paper. Fedosov [6], Kac [8] and McKean–Singer [13] recognised that certain heat trace coefficients, in particular the coefficient of t0, are not continuous as ε ↘ 0. We describe this anomaly using renormalized heat invariants of an auxiliary smooth domain Z which models the corner formation. The result applies to both Dirichlet and Neumann boundary conditions. We also include a discussion of what one might expect in higher dimensions.
${\mathcal C}$∞ boundary which converges to Ω0 smoothly away from the corners, and in a precise way at the vertices to be described in the paper. Fedosov [6], Kac [8] and McKean–Singer [13] recognised that certain heat trace coefficients, in particular the coefficient of t0, are not continuous as ε ↘ 0. We describe this anomaly using renormalized heat invariants of an auxiliary smooth domain Z which models the corner formation. The result applies to both Dirichlet and Neumann boundary conditions. We also include a discussion of what one might expect in higher dimensions.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 2 , September 2015 , pp. 303 - 319
- Copyright
- Copyright © Cambridge Philosophical Society 2015
References
REFERENCES
- 11
- Cited by


