Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-10T14:51:49.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff dimension of level sets of generalized Takagi functions

Published online by Cambridge University Press:  19 June 2014

PIETER C. ALLAART
PIETER C. ALLAART*
Affiliation:
Department of Mathematics, University of North Texas, 1155 Union Circle #311430, Denton, TX 76203-5017, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper examines the Hausdorff dimension of the level sets f−1(y) of continuous functions of the form

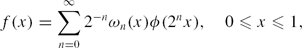\begin{equation*} f(x)=\sum_{n=0}^\infty 2^{-n}\omega_n(x)\phi(2^n x), \quad 0\leq x\leq 1, \end{equation*}
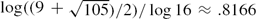where φ(x) is the distance from x to the nearest integer, and for each n, ωn is a {−1,1}-valued function which is constant on each interval [j/2n,(j+1)/2n), j=0,1,. . .,2n − 1. This class of functions includes Takagi's continuous but nowhere differentiable function. It is shown that the largest possible Hausdorff dimension of f−1(y) is $\log ((9+\sqrt{105})/2)/\log 16\approx .8166$, but in case each ωn is constant, the largest possible dimension is 1/2. These results are extended to the intersection of the graph of f with lines of arbitrary integer slope. Furthermore, two natural models of choosing the signs ωn(x) at random are considered, and almost-sure results are obtained for the Hausdorff dimension of the zero set and the set of maximum points of f. The paper ends with a list of open problems.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 157 , Issue 2 , September 2014 , pp. 253 - 278
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abbott, S., Anderson, J. M. and Pitt, L. D.Slow points for functions in the Zygmund class Λd*. Real Anal. Exchange 32 (2006/07), no. 1, 145–170.Google Scholar
[2]Allaart, P. C.Distribution of the extrema of random Takagi functions. Acta Math. Hungar. 121 (2008), no. 3, 243–275.Google Scholar
[3]Allaart, P. C.The finite cardinalities of level sets of the Takagi function. J. Math. Anal. Appl. 388 (2012), 1117–1129.Google Scholar
[4]Allaart, P. C.How large are the level sets of the Takagi function? Monatsh. Math. 167 (2012), 311–331.Google Scholar
[5]Allaart, P. C.Level sets of signed Takagi functions. Acta Math. Hungar. 141 (2013), no. 4, 339–352.CrossRefGoogle Scholar
[6]Allaart, P. C. Correction and strengthening of “How large are the level sets of the Takagi function?”, preprint, arXiv:1306.0167 (2013) (to appear in Monatsh. Math.).CrossRefGoogle Scholar
[7]Allaart, P. C. and Kawamura, K.The Takagi function: a survey. Real Anal. Exchange 37 (2011/12), no. 1, 1–54.Google Scholar
[8] E. de Amo, Bhouri, I., Carrillo, M. Díaz and Fernández–Sánchez, J.The Hausdorff dimension of the level sets of Takagi's function. Nonlinear Anal. 74 (2011), no. 15, 5081–5087.Google Scholar
[9]Anderson, J. M. and Pitt, L. D.Probabilistic behavior of functions in the Zygmund spaces Λ* and λ*. Proc. London Math. Soc. 59 (1989), no. 3, 558–592.Google Scholar
[10]Athreya, K. B. and Ney, P. E.Branching Processes (Dover, 2004).Google Scholar
[11]Billingsley, P.Van der Waerden's continuous nowhere differentiable function. Amer. Math. Monthly 89 (1982), no. 9, 691.Google Scholar
[12]Buczolich, Z.Irregular 1-sets on the graphs of continuous functions. Acta Math. Hungar. 121 (2008), no. 4, 371–393.Google Scholar
[13]Kahane, J.-P.Sur l'exemple, donné par M. de Rham, d'une fonction continue sans dérivée. Enseign. Math. 5 (1959), 53–57.Google Scholar
[14]Kawamura, K.On the classification of self-similar sets determined by two contractions on the plane. J. Math. Kyoto Univ. 42 (2002), 255–286.Google Scholar
[15]Kobayashi, Z.Digital sum problems for the Gray code representation of natural numbers. Interdiscip. Inform. Sci. 8 (2002), 167–175.Google Scholar
[16]Lagarias, J. C.The Takagi function and its properties. In: Functions and Number Theory and Their Probabilistic Aspects (Matsumote, K., Editor in Chief). RIMS Kokyuroku Bessatsu B34 (2012), pp. 153–189, arXiv:1112.4205v2.Google Scholar
[17]Lagarias, J. C. and Maddock, Z.Level sets of the Takagi function: local level sets. Monatsh. Math. 166 (2012), no. 2, 201–238.CrossRefGoogle Scholar
[18]Lagarias, J. C. and Maddock, Z.Level sets of the Takagi function: generic level sets. Indiana Univ. Math. J. 60 (2011), no. 6, 1857–1884.Google Scholar
[19]Maddock, Z.Level sets of the Takagi function: Hausdorff dimension. Monatsh. Math. 160 (2010), no. 2, 167–186.Google Scholar
[20]Marion, J.Mesures de Hausdorff et théorie de Perron-Frobenius des matrices non-negatives. Ann. Inst. Fourier (Grenoble) 35 (1985), 99–125.Google Scholar
[21]Mauldin, R. D. and Williams, S. C.Random recursive constructions: asymptotic geometric and topological properties. Trans. Amer. Math. Soc. 295 (1986), no. 1, 325–346.Google Scholar
[22]Mössner, B.On the joint spectral radius of matrices of order 2 with equal spectral radius. Adv. Comput. Math. 33 (2010), no. 2, 243–254.Google Scholar
[23]Rota, G.-C. and Strang, W. G.A note on the joint spectral radius. Indag. Math. 22 (1960), 379–381.CrossRefGoogle Scholar
[24]Takagi, T.A simple example of the continuous function without derivative. Phys.-Math. Soc. Japan 1 (1903), 176–177. The Collected Papers of Teiji Takagi, Kuroda, S., Ed., Iwanami (1973), 5–6.Google Scholar