Article contents
Hausdorff dimension and uniform exponents in dimension two
Published online by Cambridge University Press: 29 May 2018
Abstract
In this paper we prove that the Hausdorff dimension of the set of (nondegenerate) singular two-dimensional vectors with uniform exponent μ in (1/2, 1) is equal to 2(1 − μ) for μ ⩾ 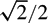 $\sqrt2/2$, whereas for μ <
$\sqrt2/2$, whereas for μ < 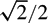 $\sqrt2/2$ it is greater than 2(1 − μ) and at most equal to (3 − 2 μ)(1 − μ)/(1 − μ + μ2). We also establish that this dimension tends to 4/3 (which is the dimension of the set of singular two-dimensional vectors) when μ tends to 1/2. These results improve upon previous estimates of R. Baker, joint work of the first author with M. Laurent, and unpublished work of M. Laurent. Moreover, we prove a lower bound for the packing dimension, which appears to be strictly greater than the Hausdorff dimension for μ ⩾ 0.565. . . .
$\sqrt2/2$ it is greater than 2(1 − μ) and at most equal to (3 − 2 μ)(1 − μ)/(1 − μ + μ2). We also establish that this dimension tends to 4/3 (which is the dimension of the set of singular two-dimensional vectors) when μ tends to 1/2. These results improve upon previous estimates of R. Baker, joint work of the first author with M. Laurent, and unpublished work of M. Laurent. Moreover, we prove a lower bound for the packing dimension, which appears to be strictly greater than the Hausdorff dimension for μ ⩾ 0.565. . . .
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 167 , Issue 2 , September 2019 , pp. 249 - 284
- Copyright
- Copyright © Cambridge Philosophical Society 2018
Footnotes
Partially supported by NSF Grant DMS 1600476.
References
REFERENCES
- 5
- Cited by


