Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T13:25:05.565Z Has data issue: false hasContentIssue false
  • English
  • Français

A harmonic quadrature formula characterizing open strips

Published online by Cambridge University Press:  24 October 2008

D. H. Armitage  and
C. S. Nelson
D. H. Armitage
Affiliation:
The Queen's University of Belfast
C. S. Nelson
Affiliation:
The Queen's University of Belfast
Get access Rights & Permissions [Opens in a new window]

Extract

Let γn denote n-dimensional Lebesgue measure. It follows easily from the well-known volume mean value property of harmonic functions that if h is an integrable harmonic function on an open ball B of centre ξ0 in ℝn, where n ≥ 2, then

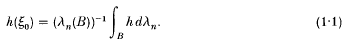
A converse of this result is due to Kuran [8]: if D is an open subset of ℝn such that γn(D) < + ∞ and if there exists a point ξo∈D such that

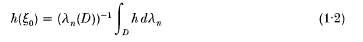
for every integrable harmonic function h on D, then D is a ball of centre ξ0. Armitage and Goldstein [2], theorem 1, showed that the same conclusion holds under the weaker hypothesis that (1·2) holds for all positive integrable harmonic functions h on D.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 1 , January 1993 , pp. 147 - 151
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aemitage, D. H. and Gardiner, S. J.. On the growth of the hyperplane mean of a subharmonic function. J. London Math. Soc. (2) 36 (1987). 501–512.CrossRefGoogle Scholar
[2]Armitage, D. H. and Goldstein, M.. The volume mean-value property of harmonic functions. Complex Variables 13 (1990), 185–193.Google Scholar
[3]Akmitage, D. H. and Goldstein, M.. Characterizations of balls and strips via harmonic quadrature. In Approximation by Solutions of Partial Differential Equations (Fuglede, B. et al. eds.), (Kluwer, 1992), pp. 1–9.Google Scholar
[4]Aemitage, D. H. and Goldstein, M.. Quadrature and harmonic approximation of sub-harmonic functions in strips. J. London Math. Soc. to appear.Google Scholar
[5]Doob, J. L.. Classical Potential Theory and its Probabilistic Counterpart (Springer-Verlag. 1984).Google Scholar
[6]Goldstein, M., Haussmann, W. and Rogge, L.. Characterization of open strips by harmonic quadrature. In Approximation by Solutions of Partial Differential Equations (Fuglede, B. et al. eds.), (Kluwer, 1992), pp. 87–92.CrossRefGoogle Scholar
[7]Goldstein, M., Haussmann, W. and Rogge, L.. On the inverse mean value property of harmonic functions on strips. Bull. London Math. Soc. 24 (1992), to appear.CrossRefGoogle Scholar
[8]Kuran, Ü.. On the mean value property of harmonic functions. Bull. London Math. Soc. 4 (1972), 311–312.CrossRefGoogle Scholar
[9]Nualtaranee, S.. On least harmonic majorants in half-spaces. Proc. London Math. Soc. (3) 27 (1973), 243–260.CrossRefGoogle Scholar
[10]Saks, S.. Theory of the Integral, 2nd ed. (Hafner, 1937).Google Scholar