No CrossRef data available.
The Hankel transform of Whittaker's function Wk, m(z)
Published online by Cambridge University Press: 24 October 2008
Extract
The Hankel transform of a function x−½νf(x) can be determined by the help of the following rule, obtained for ν = 0, 1 by B. van der Pol and K. Niessen(1), for positive integral values of ν by K. Niessen(2), and for arbitrary values of ν, [R(ν) > − 1], by F. Tricomi(3). If*
F(p) ≒ f(x),
then
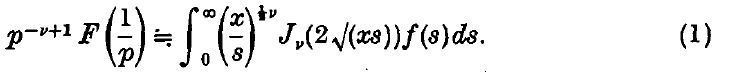
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 34 , Issue 1 , January 1938 , pp. 28 - 29
- Copyright
- Copyright © Cambridge Philosophical Society 1938
References
REFERENCES
(4)Whittaker, E. T. and Watson, G. N., Modern analysis, 4th ed. (Cambridge, 1927), chapter 16.Google Scholar
(5)Goldstein, S., Proc. London Math. Soc. (2), 34 (1932), 103, equation (80). See also Erdélyi A., Math. Zeitschrift, 42 (1936), 125, equation (2, 7).CrossRefGoogle Scholar


