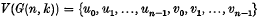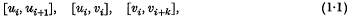Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1973.
Graphs, Groups and Surfaces.
Vol. 8,
Issue. ,
p.
279.
1981.
Zero-Symmetric Graphs.
p.
165.
Tucker, Thomas W.
1981.
Some results on the genus of a group.
Journal of Graph Theory,
Vol. 5,
Issue. 3,
p.
337.
Marušič, Dragan
1981.
On vertex symmetric digraphs.
Discrete Mathematics,
Vol. 36,
Issue. 1,
p.
69.
COXETER, H.S.M.
1986.
Symmetry.
p.
579.
Schrag, Gerald
1988.
Automorphism groups and the full state spaces of the Petersen graph generalizations of G32.
Discrete Mathematics,
Vol. 70,
Issue. 2,
p.
185.
Watkins, Mark E.
1990.
Cycles and Rays.
p.
243.
McKay, Brendan D.
and
Praeger, Cheryl E.
1994.
Vertex-transitive graphs which are not Cayley graphs, I.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 56,
Issue. 1,
p.
53.
Nedela, Roman
and
Škoviera, Martin
1995.
Which generalized petersen graphs are cayley graphs?.
Journal of Graph Theory,
Vol. 19,
Issue. 1,
p.
1.
Lovrečič Saražin, Marko
1997.
A Note on the Generalized Petersen Graphs That Are Also Cayley Graphs.
Journal of Combinatorial Theory, Series B,
Vol. 69,
Issue. 2,
p.
226.
Scapellato, Raffaele
1997.
Graph Symmetry.
p.
319.
Gamble, Greg
and
Praeger, Cheryl E.
2000.
Vertex-primitive groups and graphs of order twice the product of two distinct odd primes.
Journal of Group Theory,
Vol. 3,
Issue. 3,
Iranmanesh, Mohammad A.
and
Praeger, Cheryl E.
2001.
On Non-Cayley Vertex-Transitive Graphs of Order a Product of Three Primes.
Journal of Combinatorial Theory, Series B,
Vol. 81,
Issue. 1,
p.
1.
2001.
Graphs of Groups on Surfaces - Interactions and Models.
Vol. 188,
Issue. ,
p.
323.
White, Arthur T.
2001.
Graphs of Groups on Surfaces - Interactions and Models.
Vol. 188,
Issue. ,
p.
73.
Shim, Sangho
Širáň, Jozef
and
Žerovnik, Janez
2002.
Counterexamples to the uniform shortest path routing conjecture for vertex-transitive graphs.
Discrete Applied Mathematics,
Vol. 119,
Issue. 3,
p.
281.
Boben, Marko
Pisanski, Tomaž
and
Žitnik, Arjana
2005.
I-graphs and the corresponding configurations.
Journal of Combinatorial Designs,
Vol. 13,
Issue. 6,
p.
406.
Pedersen, J.M.
Riaz, T.M.
Knudsen, T.P.
and
Madsen, O.B.
2005.
Designing broadband access networks with triple redundancy.
p.
533.
Kutnar, Klavdija
Malnič, Aleksander
Marušič, Dragan
and
Miklavič, Štefko
2006.
Distance-balanced graphs: Symmetry conditions.
Discrete Mathematics,
Vol. 306,
Issue. 16,
p.
1881.
Širáň, Jozef
and
Tucker, Thomas W.
2007.
Characterization of graphs which admit vertex‐transitive embeddings.
Journal of Graph Theory,
Vol. 55,
Issue. 3,
p.
233.