Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Terry, C.
and
Wolf, J.
2019.
Stable arithmetic regularity in the finite field model.
Bulletin of the London Mathematical Society,
Vol. 51,
Issue. 1,
p.
70.
Terry, C.
and
Wolf, J.
2020.
Quantitative structure of stable sets in finite abelian groups.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 6,
p.
3885.
Conant, Gabriel
2020.
On finite sets of small tripling or small alternation in arbitrary groups.
Combinatorics, Probability and Computing,
Vol. 29,
Issue. 6,
p.
807.
Halevi, Yatir
Kaplan, Itay
and
Shelah, Saharon
2021.
Infinite stable graphs with large chromatic number.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 3,
p.
1767.
Conant, Gabriel
and
Pillay, Anand
2021.
Pseudofinite groups and VC-dimension.
Journal of Mathematical Logic,
Vol. 21,
Issue. 02,
p.
2150009.
Conant, Gabriel
2021.
Quantitative structure of stable sets in arbitrary finite groups.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 9,
p.
4015.
Martin-Pizarro, Amador
Palacín, Daniel
and
Wolf, Julia
2021.
A model-theoretic note on the Freiman–Ruzsa theorem.
Selecta Mathematica,
Vol. 27,
Issue. 4,
Hawthorne, Christopher
2022.
Automata and tame expansions of (ℤ, +).
Israel Journal of Mathematics,
Vol. 249,
Issue. 2,
p.
651.
Chernikov, Artem
Hrushovski, Ehud
Kruckman, Alex
Krupiński, Krzysztof
Moconja, Slavko
Pillay, Anand
and
Ramsey, Nicholas
2023.
Invariant measures in simple and in small theories.
Journal of Mathematical Logic,
Vol. 23,
Issue. 02,
Conant, Gabriel
and
Pillay, Anand
2024.
Approximate subgroups with bounded VC-dimension.
Mathematische Annalen,
Vol. 388,
Issue. 1,
p.
1001.
Martin-Pizarro, Amador
and
Palacín, Daniel
2024.
Complete type amalgamation for nonstandard finite groups.
Model Theory,
Vol. 3,
Issue. 1,
p.
1.
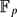 $\mathbb{F}_p$.
$\mathbb{F}_p$.

