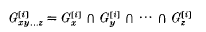Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Трофимов, Владимир Иванович
and
Trofimov, Vladimir Ivanovich
1998.
Графы с проективными подорбитами. Исключительные случаи характеристики 2. I.
Известия Российской академии наук. Серия математическая,
Vol. 62,
Issue. 6,
p.
159.
Conder, Marston D.
Li, Cai Heng
and
Praeger, Cheryl E.
2000.
On the Weiss conjecture for finite locally primitive graphs.
Proceedings of the Edinburgh Mathematical Society,
Vol. 43,
Issue. 1,
p.
129.
Li, Cai
2004.
Finite 𝑠-arc transitive Cayley graphs and flag-transitive projective planes.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 1,
p.
31.
VERRET, GABRIEL
2009.
ON THE ORDER OF ARC-STABILIZERS IN ARC-TRANSITIVE GRAPHS.
Bulletin of the Australian Mathematical Society,
Vol. 80,
Issue. 3,
p.
498.
TROFIMOV, V. I.
and
WEISS, R. M.
2010.
The group E6(q) and graphs with a locally linear group of automorphisms.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 148,
Issue. 1,
p.
1.
Spiga, Pablo
2011.
On G-locally primitive graphs of locally Twisted Wreath type and a conjecture of Weiss.
Journal of Combinatorial Theory, Series A,
Vol. 118,
Issue. 8,
p.
2257.
Morgan, G.L.
2013.
On symmetric and locally finite actions of groups on the quintic tree.
Discrete Mathematics,
Vol. 313,
Issue. 21,
p.
2486.
Giudici, Michael
and
Morgan, Luke
2014.
A class of semiprimitive groups that are graph‐restrictive.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 6,
p.
1226.
Giudici, Michael
and
Morgan, Luke
2015.
On locally semiprimitive graphs and a theorem of Weiss.
Journal of Algebra,
Vol. 427,
Issue. ,
p.
104.
Morgan, Luke
Swartz, Eric
and
Verret, Gabriel
2016.
On 2-arc-transitive graphs of order kp.
Journal of Combinatorial Theory, Series B,
Vol. 117,
Issue. ,
p.
77.
Giudici, Michael
and
Morgan, Luke
2018.
A theory of semiprimitive groups.
Journal of Algebra,
Vol. 503,
Issue. ,
p.
146.
Caprace, Pierre-Emmanuel
2019.
Groups St Andrews 2017 in Birmingham.
p.
16.
Caprace, Pierre-Emmanuel
and
Le Boudec, Adrien
2019.
Bounding the covolume of lattices in products.
Compositio Mathematica,
Vol. 155,
Issue. 12,
p.
2296.
Morgan, Luke
Praeger, Cheryl E.
and
Rosa, Kyle
2020.
Bounds for finite semiprimitive permutation groups: order, base size, and minimal degree.
Proceedings of the Edinburgh Mathematical Society,
Vol. 63,
Issue. 4,
p.
1071.
Caprace, Pierre-Emmanuel
2022.
A radius 1 irreducibility criterion for lattices in products of trees.
Annales Henri Lebesgue,
Vol. 5,
Issue. ,
p.
643.
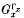 the permutation group induced on Γx. by the stabilizer Gx. For each i ≥ 1,
the permutation group induced on Γx. by the stabilizer Gx. For each i ≥ 1, 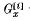 will denote the pointwise stabilizer in Gx of the set of vertices at distance at most i from x in Γ. Let
will denote the pointwise stabilizer in Gx of the set of vertices at distance at most i from x in Γ. Let