Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T12:27:12.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry of the augmented disk graph

Published online by Cambridge University Press:  02 January 2014

JIMING MA
JIMING MA*
Affiliation:
School of Mathematical Sciences, Fudan University, Shanghai, China, 200433. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a handlebody H, we define two graphs, the augmented disk graph 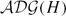$\mathcal{ADG}(H)$ and the truncated augmented disk graph 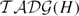$\mathcal{TADG}(H)$, and we show they are hyperbolic in the sense of Gromov. In the process, we show they are quasi-isometric to two other disk graphs defined by U. Hamenstädt, the super conducting disk graph 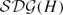$\mathcal{SDG}(H)$ and the electrified disk graph 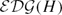$\mathcal{EDG}(H)$ respectively. So we reprove two theorems of Hamenstädt [12].

Our approach uses techniques from Masur–Schleimer's study on the hyperbolicity of the disk graph 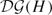$\mathcal{DG}(H)$ [21].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 2 , March 2014 , pp. 363 - 382
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aougab, T.Uniform hyperbolicity of the graphs of curves. Geom. Topo. 17 (2013), 2855–2875.Google Scholar
[2]Aougab, T. Quadratic bounds on the quasiconvexity of nested train track sequences. arXiv:math.GT/1306.1428.Google Scholar
[3]Bestvina, M. and Fujiwara, K.Quasi-homomorphisms on mapping class groups. Glas. Mat. Ser. III 42 (62) (2007), 213–236.Google Scholar
[4]Brock, J. and Farb, B.Curvature and rank of Teichmüller space. Amer. J. Math. 128 (2006), no. 1, 1–22.CrossRefGoogle Scholar
[5]Bowditch, B.Intersection numbers and the hyperbolicity of the curve complex. J. Reine Angew. Math. 598 (2006), 105–129.Google Scholar
[6]Bowditch, B. Uniform hyperbolicity of the curve graphs, to appear in Pacific J. Math.Google Scholar
[7]Clay, M., Rafi, K. and Schleimer, S. Uniform hyperbolicity of the curve graph via surgery sequences, arXiv:math.GT/1302.5519.Google Scholar
[8]Farb, B.Relatively hyperbolic groups. Geom. Funct. Anal. 8 (1998), no. 5, 810–840.Google Scholar
[9]Hamenstädt, U.Geometry of the complex of curves and of Teichmüller space. In Handbook of Teichmüller theory. vol. I, IRMA Lect. Math. Theor. Phys. 11 (Eur. Math. Soc., Zürich. 2007), PP. 447–467.Google Scholar
[10]Hamenstädt, U.Train tracks and the Gromov boundary of the complex of curves. In Spaces of Kleinian Groups Minsky, Y., Sakuma, M. and Series, C., eds. London Math. Soc. Lecture Notes 329 (2005), 187–207.Google Scholar
[11]Hamenstädt, U.Geometry of the mapping class groups I: boundary amenability. Invent. Math. 175 (2009), 545–609.Google Scholar
[12]Hamenstädt, U. Geometry of graphs of discs in a handlebody. arXiv:math.GT/1101.1843, version 2 (June 2011) and version 3 (March, 2013).Google Scholar
[13]Harvey, W.Boundary structure of the modular group. In Riemann Surfaces and Related topics. Ann. of Math. Stud., vol. 97 (Princeton University Press, 1981), PP. 245–251.Google Scholar
[14]Hempel, J.3-manifolds as viewed from the curve complex. Topology 40 (2001), 631–657.Google Scholar
[15]Hensel, S., Przytycki, P. and Webb, R. Slim unicorns and uniform hyperbolicity for arc graphs and curve graphs. To appear in J. Eur. Math. Soc.Google Scholar
[16]Klarreich, E. The boundary at infinity of the curve complex and the relative Teichmüller space. Unpublished manuscript (Ann Arbor 1999).Google Scholar
[17]Masur, H.Measured foliations and handlebodies. Ergodic Theory Dynam. Systems 6 (1986), 99–116.Google Scholar
[18]Masur, H. and Minsky, Y.Geometry of the complex of curves. I. Hyperbolicity. Invent. Math. 138 (1999), 103–149.Google Scholar
[19]Masur, H. and Minsky, Y.Geometry of the complex of curves. II. Hierarchical structure. Geom. Funct. Anal. 10 (2000), 902–974.CrossRefGoogle Scholar
[20]Masur, H. and Minsky, Y.Quasiconvexity in the curve complex. In the Tradition of Ahlfors and Bers, III, Abikoff, W. and Haas, A., eds. Contemp. Math. 55 (Amer. Math. Soc., 2004), 309–320.Google Scholar
[21]Masur, H. and Schleimer, S.The geometry of the disk complex. J. Amer. Math. Soc. 26 (2013), 1–62.CrossRefGoogle Scholar
[22]Minsky, Y.The classification of Kleinian surface groups I: models and bounds. Ann. of Math. 171 (2010), 1–107.CrossRefGoogle Scholar
[23]Mj, M.Mapping class groups and interpolating complex: rank. J. Ramanujan Math. Soc. 4 (2009), 341–357.Google Scholar
[24]Webb, R. Uniform bounds for bounded geodesic image theorems. To appear in J. Reine. Angew. Math.Google Scholar