Published online by Cambridge University Press: 24 October 2008
§ 1. The six Plücker coordinates of a straight line in three dimensional space satisfy an identical quadratic relation
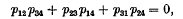
which immediately shows that a one-one correspondence may be set up between lines in three dimensional space, λ, and points on a quadric manifold 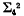 of four dimensions in five dimensional space, S5. For these six numbers pij may be considered to be six homogeneous coordinates of such a point.
of four dimensions in five dimensional space, S5. For these six numbers pij may be considered to be six homogeneous coordinates of such a point.
* It seems unnecessary here to develop the pure geometrical theory of negative circles in full. It corresponds to the analytical fact that a locus
exists where g, f, c are real and g2 + f2 < c.
† Cf. Baker, , Principles of Geometry, I (Cambridge, 1922), 165–172, 182.Google Scholar
* One system of generators of an ordinary ruled quadrio surface.