Article contents
Geometric collections and Castelnuovo–Mumford regularity
Published online by Cambridge University Press: 01 November 2007
Abstract
The paper begins by overviewing the basic facts on geometric exceptional collections. Then we derive, for any coherent sheaf 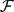 on a smooth projective variety with a geometric collection, two spectral sequences: the first one abuts to
on a smooth projective variety with a geometric collection, two spectral sequences: the first one abuts to 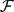 and the second one to its cohomology. The main goal of the paper is to generalize Castelnuovo–Mumford regularity for coherent sheaves on projective spaces to coherent sheaves on smooth projective varieties X with a geometric collection σ. We define the notion of regularity of a coherent sheaf
and the second one to its cohomology. The main goal of the paper is to generalize Castelnuovo–Mumford regularity for coherent sheaves on projective spaces to coherent sheaves on smooth projective varieties X with a geometric collection σ. We define the notion of regularity of a coherent sheaf 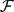 on X with respect to σ. We show that the basic formal properties of the Castelnuovo–Mumford regularity of coherent sheaves over projective spaces continue to hold in this new setting and we show that in case of coherent sheaves on
on X with respect to σ. We show that the basic formal properties of the Castelnuovo–Mumford regularity of coherent sheaves over projective spaces continue to hold in this new setting and we show that in case of coherent sheaves on 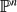 and for a suitable geometric collection of coherent sheaves on
and for a suitable geometric collection of coherent sheaves on 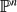 both notions of regularity coincide. Finally, we carefully study the regularity of coherent sheaves on a smooth quadric hypersurface
both notions of regularity coincide. Finally, we carefully study the regularity of coherent sheaves on a smooth quadric hypersurface 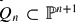 (n odd) with respect to a suitable geometric collection and we compare it with the Castelnuovo–Mumford regularity of their extension by zero in
(n odd) with respect to a suitable geometric collection and we compare it with the Castelnuovo–Mumford regularity of their extension by zero in 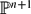 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 143 , Issue 3 , November 2007 , pp. 557 - 578
- Copyright
- Copyright © Cambridge Philosophical Society 2007
References
REFERENCES
- 5
- Cited by


