Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T13:38:03.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Schwarzian derivatives and higher order differential equations

Published online by Cambridge University Press:  20 June 2011

MARTIN CHUAQUI ,
JANNE GRÖHN  and
JOUNI RÄTTYÄ
MARTIN CHUAQUI
Affiliation:
P. Universidad Católica de Chile, Av. Vicuña Mackenna 4860, Santiago, Chile. e-mail: [email protected]
JANNE GRÖHN
Affiliation:
University of Eastern Finland, Campus of Joensuu, P.O. Box 111, 80101 Joensuu, Finland. e-mail: [email protected] and [email protected]
JOUNI RÄTTYÄ
Affiliation:
University of Eastern Finland, Campus of Joensuu, P.O. Box 111, 80101 Joensuu, Finland. e-mail: [email protected] and [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that the well-known connection between the second order linear differential equation h″ + B(z)h = 0, with a solution base {h1, h2}, and the Schwarzian derivative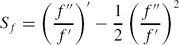of f = h1/h2, can be extended to the equation h(k) + B(z) h = 0 where k ≥ 2. This generalization depends upon an appropriate definition of the generalized Schwarzian derivative Sk(f) of a function f which is induced by k−1 ratios of linearly independent solutions of h(k) + B(z) h = 0. The class 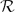k(Ω) of meromorphic functions f such that Sk(f) is analytic in a given domain Ω is also completely described. It is shown that if Ω is the unit disc 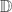or the complex plane 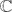, then the order of growth of f ∈ 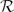k(Ω) is precisely determined by the growth of Sk(f), and vice versa. Also the oscillation of solutions of h(k) + B(z) h = 0, with the analytic coefficient B in 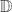or , in terms of the exponent of convergence of solutions is briefly discussed.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 151 , Issue 2 , September 2011 , pp. 339 - 354
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Astala, K. and Zinsmeister, M.Teichmüller spaces and BMOA. Math. Ann. 289 (1991), no. 4, 613–625.CrossRefGoogle Scholar
[2]Bank, S.A general theorem concerning the growth of solutions of first-order algebraic differential equations. Compositio Math. 25 (1972), no. 1, 61–70.Google Scholar
[3]Bertilsson, D.Coefficient estimates for negative powers of the derivative of univalent functions. Ark. Mat. 36 (1998), no. 2, 255–273.CrossRefGoogle Scholar
[4]Bishop, C. J. and Jones, P. W.Harmonic measure, L 2 estimates and the Schwarzian derivative. J. Anal. Math. 62 (1994), 77–113.CrossRefGoogle Scholar
[5]Cartwright, M. L.On analytic functions regular in the unit circle (II). Quart. J. Math. 4 (1933), 246–257.Google Scholar
[6]Chyzhykov, I., Heittokangas, J. and Rättyä, J.Finiteness of ϕ-order of solutions of linear differential equations in the unit disc. J. Anal. Math. 109 (2009), 163–198.CrossRefGoogle Scholar
[7]Chyzhykov, I., Heittokangas, J. and Rättyä, J.Sharp logarithmic derivative estimates with applications to ordinary differential equations in the unit disc. J. Aust. Math. Soc. 88 (2010), no. 2, 145–167.CrossRefGoogle Scholar
[8]Gundersen, G. G.Finite order solutions of second order linear differential equations. Trans. Amer. Math. Soc. 305 (1988), no. 1, 415–429.CrossRefGoogle Scholar
[9]Gundersen, G. G., Steinbart, E. M. and Wang, S.The possible orders of solutions of linear differential equations with polynomial coefficients. Trans. Amer. Math. Soc. 350 (1998), no. 3, 1225–1247.CrossRefGoogle Scholar
[10]Heittokangas, J. and Rättyä, J.Zero distribution of solutions of complex linear differential equations determines growth of coefficients. Math. Nachr. 284 (2011), no. 4, 412–420.CrossRefGoogle Scholar
[11]Heittokangas, J., Korhonen, R. and Rättyä, J.Growth estimates for solutions of linear complex differential equations. Ann. Acad. Sci. Fenn. Math. 29 (2004), no. 1, 233–246.Google Scholar
[12]Heittokangas, J., Korhonen, R. and Rättyä, J.Linear differential equations with coefficients in the weighted Bergman and Hardy spaces. Trans. Amer. Math. Soc. 360 (2008), 1035–1055.CrossRefGoogle Scholar
[13]Kim, W. J.The Schwarzian derivative and multivalence. Pacific J. Math. 31 (1969), 717–724.CrossRefGoogle Scholar
[14]Korhonen, R. and Rättyä, J.Finite order solutions of linear differential equations in the unit disc. J. Math. Anal. Appl. 349 (2009), no. 1, 43–54.CrossRefGoogle Scholar
[15]Laine, I.Nevanlinna Theory and Complex Differential Equations (Walter de Gruyter, Berlin, 1993).CrossRefGoogle Scholar
[16]Pau, J. and Peláez, J. A.Logarithms of the derivative of univalent functions in Q p spaces. J. Math. Anal. Appl. 350 (2009), 184–194.CrossRefGoogle Scholar
[17]Pérez-González, F. and Rättyä, J.Dirichlet and VMOA domains via Schwarzian derivative. J. Math. Anal. Appl. 359 (2009), 543–546.CrossRefGoogle Scholar
[18]Pommerenke, Ch.Boundary Behaviour of Conformal Maps. (Springer-Verlag, Berlin, 1992).CrossRefGoogle Scholar
[19]Schippers, E.Distortion theorems for higher order Schwarzian derivatives of univalent functions. Proc. Amer. Math. Soc. 128 (2000), no. 11, 3241–3249.CrossRefGoogle Scholar
[20]Wittich, H.Zur theorie linearer differentialgleichungen im komplexen. Ann. Acad. Sci. Fenn. Ser. A I Math. 379 (1966), 1–18.CrossRefGoogle Scholar