Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T11:43:53.950Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Gâteaux and Fréchet derivatives in convolution algebras

Published online by Cambridge University Press:  24 October 2008

J. B. Miller
J. B. Miller
Affiliation:
Department of Mathematics, Australian National University, Canberra, and Yale University
Get access Rights & Permissions [Opens in a new window]

Extract

Let 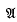be a commutative normed algebra whose elements are functions on a Banach space, and in which the product is of convolution type. We show how 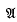, under reasonable assumptions upon its semi-group of translation operators and rather severe restrictions upon its semi-simplicity, can be renormed so that its completion contains mean Gâteaux or Fréchet differentials of all its members. In this way the function algebra 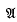can be embedded in an algebra of generalized functions defined as strong limits of functions, which admits strong differentiation as an everywhere-defined operation. The differentials show most of the properties of point-wise Gâteaux differentials. The completion of 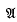is an example of what I have called in (3) an ‘inflation’.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 4 , October 1963 , pp. 707 - 718
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hille, E. and Phillips, R. S.Functional analysis and semi-groups (revised ed.), Providence, R.I. (American Mathematical Society Colloquium Publication, xxxi; 1957).Google Scholar
(2)kelley, J. L.General topology (Van Nostrand; New York, 1955).Google Scholar
(3)Miller, J. B.Normed spaces of generalized functions. Compositio Math. (to appear).Google Scholar
(4)Rickart, C. E.General theory of Banach algebras (Van Nostrand; Princeton, 1960).Google Scholar
(5)Wendel, J. G.Left centralizers and isomorphisms of group algebras. Pacific J. Math. 2 (1952), 251–261CrossRefGoogle Scholar
(6)Weston, J. D.Positive perfect operators. Proc. London Math. Soc. (3), 10 (1960), 545–565CrossRefGoogle Scholar