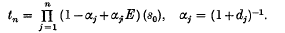Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-18T07:23:51.283Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalization of the Sα-summation method

Published online by Cambridge University Press:  24 October 2008

A. Meir  and
A. Sharma
A. Meir
Affiliation:
University of Alberta
A. Sharma
Affiliation:
University of Alberta
Get access Rights & Permissions [Opens in a new window]

Extract

In 1949, Meyer-König (5) introduced the so-called Sα-method of summability which is one of a family of transformations including the Euler, Borel and Taylor methods. Later in 1959, Jakimowski (3) defined the [F, dn] transformation which includes the Euler method as a special case. If {dn} is given infinite sequence and E denotes the displacement operator (i.e. Eks0 = sk), then the [F, dn] transformation of {sn} is given by {tn} where

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 1 , January 1970 , pp. 61 - 66
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

(1)Agnew, R. P.Euler transformations. Amer. J. Math. 66 (1944), 313–337.Google Scholar
(2)Ishiguro, K.Über das S α-Verfahren bei Fourier–Reihen. Math. Z. 80 (1962) 44–11.CrossRefGoogle Scholar
(3)Jakimovski, A.A generalization of the Lototsky method of summability. Michigan Math. J. 6 (1959), 277–290.CrossRefGoogle Scholar
(4)Lorch, L. and Newman, D. J.On the [F, d n]-summation of Fourier Series. Comm. Pure Appl. Math. 15 (1962), 109–118.CrossRefGoogle Scholar
(5)Meybb-König, W.Untersuchungen über einige verwandte Limitierungsverfahren. Math. Z.. 52 (1950), 257–304.CrossRefGoogle Scholar