Let G be an infinite partially directed graph of finite outgoing degree. Thus G consists of an infinite set of vertices, together with a set of edges between certain prescribed pairs of vertices. Each edge may be directed or undirected, and the number of edges from (but not necessarily to) any given vertex is always finite (though possibly unbounded). A path on G from a vertex V1 to a vertex Vn (if such a path exists) is a finite sequence of alternate edges and vertices of the form E12, V2, E23, V3, …, En − 1, n, Vn such that Ei, i + 1 is an edge connecting Vi and Vi + 1 (and in the direction from Vi to Vi + 1 if that edge happens to be directed). In mixed Bernoulli percolation, each vertex Vi carries a random variable di, and each edge Eij carries a random variable dij. All these random variables di and dij are mutually independent, and take only the values 0 or 1; the di take the value 1 with probability p, while the dij take the value 1 with probability p. A path is said to be open if and only if all the random variables carried by all its edges and all its vertices assume the value 1. Let S be a given finite set of vertices, called the source set; and let T be the set of all vertices such that there exists at least one open path from some vertex of S to each vertex of T. (We imagine that fluid, supplied to all the source vertices, can flow along any open path; and thus T is the random set of vertices eventually wetted by the fluid). The percolation probability

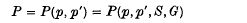
is defined to be the probability that T is an infinite set.