Generalization of Hölder's and Minkowski's inequalities
Published online by Cambridge University Press: 24 October 2008
Extract
In a recent paper (1) the authors considered some generalizations of Cauchy's inequality. The method of approach was by the construction of certain convex functions (where by a convex function we mean a function f(x) satisfying
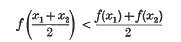
for every pair of unequal values x1 and x2). For example, it was shown that if (a), (b) are the sets of non-negative real numbers a1, …,an; bl, …, bn, the function
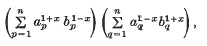
which had been used earlier by Callebaut(2), is a convex function with minimum at x = 0, except if the sets (a) and (b) are proportional, in which case the function is a constant. This function takes the value (σab)2 when x = 0 and (σa2) (Σb2) when x = 1, and the property of convexity gives Cauchy's inequality.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 4 , October 1968 , pp. 1023 - 1027
- Copyright
- Copyright © Cambridge Philosophical Society 1968
References
REFERENCES
- 14
- Cited by


