Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T07:53:29.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Fourier series associated with the sample functions of a stochastic process

Published online by Cambridge University Press:  24 October 2008

G. Samal
G. Samal
Affiliation:
Department of Mathematics, Ravenshaw College, Cuttack 3, Orissa, India
Get access Rights & Permissions [Opens in a new window]

Extract

We consider a stochastically continuous process ω(t, α) with independent increments, whose sample functions are bounded in the unit interval 0 ≤ t ≤ 1 for almost all α. If ω(t, α) is a process with independent increments, the characteristic function of ω(t, α) is of the form exp {tψ(u)} where 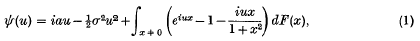where F is a σ-finite measure with finite mass outside every neighbourhood of o, and a and σ are constants. There is no essential restriction in supposing ω(0, α) = 0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 1 , January 1970 , pp. 101 - 106
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cramer, H.Random variables and probability distribution. Cambridge Tracts in Mathematics. No. 36, (Cambridge University Press, 1937).Google Scholar
(2)Gikhman, & Skorohod, . Introduction to the theory of random processes (In Russian), Izdatelstvo Nauka (Moscow, 1965).Google Scholar
(3)Gnedenko, B. V. & Kolmogorov, A. N.Limit distributions for sums of independent random variables (Addison-Wesley, Inc., 1954).Google Scholar
(4)Samal, G. Ph.D. thesis, London University (1961).Google Scholar