Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T13:30:23.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite propagation speed and Connes' foliation algebra

Published online by Cambridge University Press:  24 October 2008

John Roe
John Roe
Affiliation:
Mathematical Institute, University of Oxford
Get access Rights & Permissions [Opens in a new window]

Extract

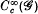In [4], A. Connes has defined the convolution algebra associated to a foliation ℱ of the compact manifold M. Here 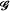is the graph or holonomy groupoid of the foliation ℱ (Winkelnkemper [15]). By forming the completion of 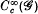in its regular representation, he obtains the C*-algebra C*{M, ℱ) associated to the foliation. The completeness of C*(M, ℱ) makes it easier to handle in some analytical contexts, but in others it seems to be too big, and it is necessary to consider instead some carefully selected dense subalgebra (cf. [6]). The purpose of this note is to show that certain spectral functions of leafwise elliptic operators, which might a priori be expected to belong to C*(M, ℱ), in fact belong to the more controllable dense subalgebra 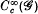. We give a couple of applications, including a proof not passing through C*-algebras of Connes' index theorem for measured foliations [4]. It should be emphasized that the proof of that result offered here is essentially Connes' one, but the presentation may perhaps be more congenial to those who are not C*-algebra specialists.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 459 - 466
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F., Bott, R. and Patodi, V. K.. On the heat equation and the index theorem. Invent. Math. 19 (1973), 279–330.CrossRefGoogle Scholar
[2]Cheeger, J., Gromov, M. and Taylor, M.. Finite propagation speed, kernel estimates for functions of the Laplace operator, and the geometry of complete Riemannian manifolds. J. Differential Geom. 17 (1982), 15–54.CrossRefGoogle Scholar
[3]Chernoff, P. R.. Essential self-adjointness of powers of generators of hyperbolic equations. J. Funct. Anal. 12 (1973), 401–414.CrossRefGoogle Scholar
[4]Connes, A.. Sur la théorie non-commutative de l'intégration. In Algèbres d'opérateurs, Springer Lecture Notes in Math. Vol. 725 (1979), 19–143.CrossRefGoogle Scholar
[5]Connes, A., A survey of foliations and operator algebras. In Proceedings of the Kingston Conference on Operator Algebras, AMS Proc. Symp. Pure. Math. 38 (1982), 521–628.Google Scholar
[6]Connes, A.. The transverse fundamental class of a foliation. IHES preprint (1984).Google Scholar
[7]Dixmier, J.. Les algèbres d'opérateurs dans l'espace Hilbertien (Gauthier-Villars, 1969).Google Scholar
[8]Garnett, L.. Functions and measures harmonic along the leaves of a foliation and the ergodic theorem. J. Funct. Anal. 51 (1983), 285–311.CrossRefGoogle Scholar
[9]Gilkey, P. B.. The heat equation and the index theorem (Publish or Perish, 1977).Google Scholar
[10]Gromov, M. and Lawson, B.. Positive scalar curvature and the Dirac operator. Publ. Math. IHES 58 (1983), 83–196.CrossRefGoogle Scholar
[11]John, F.. Partial Differential Equations (Springer-Verlag, 1982).CrossRefGoogle Scholar
[12]Roe, J.. An index theorem on open manifolds I, J. Diff. Geom., to appear.Google Scholar
[13]Roe, J.. An index theorem on open manifolds II, J. Diff. Geom., to appear.Google Scholar
[14]Taylor, M.. Pseudo-differential operators (Princeton, 1982).Google Scholar
[15]Winkelnkemper, H.. The graph of a foliation. Ann. Global Anal, and Geom. 1 (1983), 51–75.Google Scholar
[16]Yosida, K.. Functional Analysis (Springer-Verlag, 1980).Google Scholar