No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let K be a field with char K ≡ 2,3. We consider the problem of finding rational points over K on the family of elliptic curves Fλ, given in homogeneous coordinates (over 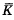 ) by
) by