Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-29T19:45:02.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Essentially unbounded chains in compact sets

Published online by Cambridge University Press:  24 October 2008

D. H. Fremlin  and
K. Kunen
D. H. Fremlin
Affiliation:
Mathematics Department, University of Essex, Colchester C04 3SQ, England
K. Kunen
Affiliation:
Mathematics Department, Van Vleck Hall, University of Wisconsin, Madison, WI 53706, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

We discuss the possible cofinalities of ⊆ *-chains in 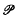ℕ which are ⊆ *-unbounded in their topological closures.

1. The problem. Throughout this paper, the power set 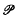ℕ of the set ℕ of natural numbers will be given its usual compact metrizable topology corresponding to the product topology of {0,1}N. We say that a ⊆ * b if a/b is finite.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 1 , January 1991 , pp. 149 - 160
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bartoszyński, T.. Additivity of measure implies additivity of category. Trans. Amer. Math. Soc. 281 (1984), 209–213.Google Scholar
[2]Baumgartner, J. E.. Applications of the proper forcing axiom (pp. 913–960 in [10]).CrossRefGoogle Scholar
[3]van Douwen, E. K.. The integers and topology (pp. 111–168 in [10]).Google Scholar
[4]Fremlin, D. H.. Consequences of Martin's Axiom (Cambridge University Press, 1984).CrossRefGoogle Scholar
[5]Fremlin, D. H.. Cichoń's Diagram. Séminaire d'initiation à l'analyse (Choquet, G., Rogalski, M., Saint-Raymond, J.), Univ. Pierre et Marie Curie, Paris 23 (1985), 5.01–5.13.Google Scholar
[6]Fremlin, D. H.. Measure Algebras (pp. 878–980 in [11]).Google Scholar
[7]Hausdorff, F.. Summen von ℵ1 Mengen. Fund. Math. 26 (1936), 241–255.CrossRefGoogle Scholar
[8]Kunen, K.. Inaccessibility properties of cardinals. Ph.D. thesis, Stanford University (1968).Google Scholar
[9]Kunen, K.. Set Theory (North-Holland, 1980).Google Scholar
[10]Kenun, K. and Vaughan, J. E. (editors). Handbook of Set-Theoretic Topology (North-Holland, 1984).Google Scholar
[11]Monk, J. D. (editor). Handbook of Boolean Algebra (North-Holland, 1989).Google Scholar
[12]Scott, D. S. (editor). Axiomatic Set Theory. (Proc. Symposia Pure Math. vol. 13, American Mathematical Society, 1971).Google Scholar
[13]Solovay, R. M.. Real-valued measurable cardinals (pp. 397–428 in [12]).Google Scholar
[14]Weiss, W.. Versions of Martin's Axiom (pp. 827–886 in [10]).CrossRefGoogle Scholar