Published online by Cambridge University Press: 05 May 2010
We establish two embedding theorems for tree-free groups. The first result embeds a group G acting freely and without inversions on a Λ-tree X into a group 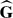 acting freely, without inversions, and transitively on a Λ-tree
acting freely, without inversions, and transitively on a Λ-tree 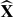 in such a way that X embeds into
in such a way that X embeds into 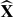 by means of a G-equivariant isometry. The second result embeds a group G acting freely and transitively on an ℝ-tree X into
by means of a G-equivariant isometry. The second result embeds a group G acting freely and transitively on an ℝ-tree X into 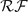 (H) for some suitable group H, again in such a way that X embeds G-equivariantly into the ℝ-tree XH associated with
(H) for some suitable group H, again in such a way that X embeds G-equivariantly into the ℝ-tree XH associated with 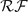 (H). The group
(H). The group 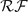 (H) referred to here belongs to a class of groups introduced and studied by the present authors in [3]. As a consequence of these two theorems, we find that
(H) referred to here belongs to a class of groups introduced and studied by the present authors in [3]. As a consequence of these two theorems, we find that 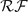 -groups and their associated ℝ-trees are in fact universal for free ℝ-tree actions. Moreover, our first embedding theorem throws light on the question, arising from the results of [7], whether a group endowed with a Lyndon length function L can always be embedded in a length-preserving way into a group with a regular Lyndon length function; modulo an obvious necessary restriction we show that this is indeed the case if L is free.
-groups and their associated ℝ-trees are in fact universal for free ℝ-tree actions. Moreover, our first embedding theorem throws light on the question, arising from the results of [7], whether a group endowed with a Lyndon length function L can always be embedded in a length-preserving way into a group with a regular Lyndon length function; modulo an obvious necessary restriction we show that this is indeed the case if L is free.