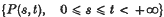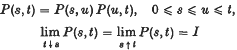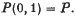Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Frydman, Halina
1980.
A structure of the Bang-Bang representation for 3�3 embeddable matrices.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 53,
Issue. 3,
p.
305.
Singer, Burton
1982.
Aspects of non-stationarity.
Journal of Econometrics,
Vol. 18,
Issue. 1,
p.
169.
Frydman, Halina
1985.
A structure of doubly stochastic Markov chains.
Linear Algebra and its Applications,
Vol. 67,
Issue. ,
p.
51.
Kalbfleisch, J. D.
and
Lawless, J. F.
1985.
The Analysis of Panel Data under a Markov Assumption.
Journal of the American Statistical Association,
Vol. 80,
Issue. 392,
p.
863.
Fuglede, B.
1988.
On the imbedding problem for stochastic and doubly stochastic matrices.
Probability Theory and Related Fields,
Vol. 80,
Issue. 2,
p.
241.
Carette, Philippe
1999.
Modelling hierarchical systems by a continuous-time homogeneous Markov chain using two-wave panel data.
Journal of Applied Probability,
Vol. 36,
Issue. 3,
p.
644.
Carette, Philippe
1999.
Modelling hierarchical systems by a continuous-time homogeneous Markov chain using two-wave panel data.
Journal of Applied Probability,
Vol. 36,
Issue. 03,
p.
644.
2004.
Encyclopedia of Statistical Sciences.
2005.
Encyclopedia of Statistical Sciences.
Chen, Yong
and
Chen, Jianmin
2011.
On the Imbedding Problem for Three-State Time Homogeneous Markov Chains with Coinciding Negative Eigenvalues.
Journal of Theoretical Probability,
Vol. 24,
Issue. 4,
p.
928.
Verbyla, Klara L.
Yap, Von Bing
Pahwa, Anuj
Shao, Yunli
Huttley, Gavin A.
and
Scheffler, Konrad
2013.
The Embedding Problem for Markov Models of Nucleotide Substitution.
PLoS ONE,
Vol. 8,
Issue. 7,
p.
e69187.
2014.
Wiley StatsRef: Statistics Reference Online.
Rabta, Boualem
van den Boom, Bart
and
Molini, Vasco
2016.
A Continuous‐time Markov Chain Approach for Modeling of Poverty Dynamics: Application to Mozambique.
African Development Review,
Vol. 28,
Issue. 4,
p.
482.
Jia, Chen
2016.
A solution to the reversible embedding problem for finite Markov chains.
Statistics & Probability Letters,
Vol. 116,
Issue. ,
p.
122.
Hughes, Maximilian
and
Werner, Ralf
2016.
Choosing Markovian Credit Migration Matrices by Nonlinear Optimization.
Risks,
Vol. 4,
Issue. 3,
p.
31.
Guerry, Marie-Anne
2019.
Sufficient embedding conditions for three-state discrete-time Markov chains with real eigenvalues.
Linear and Multilinear Algebra,
Vol. 67,
Issue. 1,
p.
106.
Baake, Michael
and
Sumner, Jeremy
2024.
Embedding of Markov matrices for $$\varvec{d \leqslant 4}$$.
Journal of Mathematical Biology,
Vol. 89,
Issue. 2,