Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T07:43:07.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding derivatives of weighted Hardy spaces into Lebesgue spaces1

Published online by Cambridge University Press:  24 October 2008

Daniel Girela ,
María Lorente  and
María Dolores Sarrión
Daniel Girela
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071 Málaga, Spain
María Lorente
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071 Málaga, Spain
María Dolores Sarrión
Affiliation:
Departamento de Economía Aplicada (Estad. y Econom.), Facultad de C. Económicas y Empresariales, Universidad de Málaga, 29071 Málaga, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 1 ≤ p < ∞ and let ω be a non-negative function defined on the unit circle T which satisfies the Ap condition of Muckenhoupt. The weighted Hardy space Hp(ω) consists of those functions f in the classical Hardy space H1 whose boundary values belong to Lp(ω). Recently McPhail (Studia Math. 96, 1990) has characterized those positive Borel measures μ on the unit disc Δ for which Hp(ω) is continuously contained in Lp(dμ). In this paper we study the question of finding necessary and sufficient conditions on a positive Borel measure μ on Δ for the differentiation operator D defined by Df = f′ to map Hp(ω) continuously into Lp(dμ). We prove that a necessary condition is that there exists a positive constant C such that

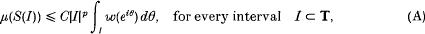
where for any interval I ⊂ T,

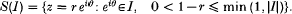
We prove that this condition is also sufficient in some cases, namely for 2 ≤ p < ∞ and ω(et0) = |θ|α, (|θ| ≤ π), – 1 < α < p – 1, but not in general. In the general case we prove the sufficiency of a condition which is slightly stronger than (A).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 116 , Issue 1 , July 1994 , pp. 151 - 166
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carleson, L.. An interpolation problem for bounded analytic functions. Amer. J. Math. 80 (1958), 921–930.CrossRefGoogle Scholar
[2]Carleson, L.. Interpolation by bounded analytic functions and the corona problem. Ann. of Math. 76 (1962), 547–559.Google Scholar
[3]Duren, P. L.. Theory of H p spaces (Academic Press, 1970).Google Scholar
[4]García-Cuerva, J. and Rubio De Francia, J. L.. Weighted norm inequalities and related topics (North-Holland, 1985).Google Scholar
[5]Girela, D.. Mean growth of the derivative of certain classes of analytic functions. Math. Proc. Cambridge Philos. Soc. 112 (1992), 335–342.CrossRefGoogle Scholar
[6]Gerela, D.. Growth of the derivative of bounded analytic functions. Complex Variables Theory Appl. 20 (1992), 221–227.Google Scholar
[7]Hunt, R., Muckenhoupt, B. and Wheeden, R.. Weighted norm inequalities for the conjugate function and Hilbert transform. Trans. Amer. Math. Soc. 176 (1973), 227–251.Google Scholar
[8]Luecking, D. H.. Embedding derivatives of Hardy spaces into Lebesgue spaces. Proc. London Math. Soc. (3) 63 (1991), 595–619.CrossRefGoogle Scholar
[9]McPhail, J. D.. A weighted interpolation problem for analytic functions. Studia Math. 96 (1990), 105–116.Google Scholar
[10]Muckenhoupt, B.. Weighted norm inequalities for the Hardy maximal function. Trans. Amer. Math. Soc. 165 (1972), 207–226.CrossRefGoogle Scholar
[11]Shirokov, N. A.. Some generalizations of the Littlewood–Paley Theorem. J. Soviet Math. 8 (1976), 119–129.CrossRefGoogle Scholar
[12]Torchinsky, A.. Real-variable methods in harmonic analysis (Academic Press, 1986).Google Scholar