Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
James, LA
and
Mills, WJ
1981.
Fatigue Crack Growth Measurement and Data Analysis.
p.
70.
Newman, J. C.
1981.
Stress-intensity factors and crack-opening displacements for round compact specimens.
International Journal of Fracture,
Vol. 17,
Issue. 6,
p.
567.
Panasyuk, V. V.
Datsyshin, A. P.
and
Rud', N. A.
1984.
Determination of the characteristics of crack resistance in off-center tension of disk samples with an edge crack.
Soviet Materials Science,
Vol. 20,
Issue. 1,
p.
16.
Kendall, K.
and
Gregory, R. D.
1987.
Fracture of radially edge-cracked discs.
Journal of Materials Science,
Vol. 22,
Issue. 12,
p.
4514.
Gregory, R. D.
1989.
The spinning circular disc with a radial edge crack; an exact solution.
International Journal of Fracture,
Vol. 41,
Issue. 1,
p.
39.
Orynyak, I. V.
1990.
Constructing the weight function for flat solids with cracks.
Strength of Materials,
Vol. 22,
Issue. 8,
p.
1117.
Wu, X. R.
1991.
The arbitrarily loaded single-edge cracked circular disc; accurate weight function solutions.
International Journal of Fracture,
Vol. 49,
Issue. 4,
p.
239.
Ma, C.-C.
and
Liao, M.-H.
1996.
Analysis of Axial Cracks in Hollow Cylinders Subjected to Thermal Shock by Using the Thermal Weight Function Method.
Journal of Pressure Vessel Technology,
Vol. 118,
Issue. 2,
p.
146.
Ciavarella, M
Demelio, G
and
Pappalettere, C
1998.
On the post-processing of data obtained from cracked components.
The Journal of Strain Analysis for Engineering Design,
Vol. 33,
Issue. 1,
p.
67.
Orynyak, I. V.
Borodii, M. V.
and
Krasovs'kyi, A. Ya
1998.
A method for the evaluation of the stress intensity factors for cracks originating from notches.
Materials Science,
Vol. 34,
Issue. 5,
p.
672.
Kendall, Kevin
2002.
Adhesion Science and Engineering.
p.
77.
Karpenko, M.
and
Wu, Q.
2003.
Photoelastic validation of a theoretical solution for an edge cracked disk.
Experimental Mechanics,
Vol. 43,
Issue. 4,
p.
410.
Donovan, J.G.
and
Karfakis, M.G.
2004.
Adaptation of a simple wedge test for the rapid determination of mode I fracture toughness and the assessment of relative fracture resistance.
International Journal of Rock Mechanics and Mining Sciences,
Vol. 41,
Issue. 4,
p.
695.
Leung, A.Y.T.
Xu, Xinsheng
Zhou, Zhenhuan
and
Wu, Y.F.
2009.
Analytic stress intensity factors for finite elastic disk using symplectic expansion.
Engineering Fracture Mechanics,
Vol. 76,
Issue. 12,
p.
1866.
Nekislykh, E. M.
and
Ostrik, V. I.
2010.
Problems on elastic equilibrium of a wedge with cracks on the axis of symmetry.
Mechanics of Solids,
Vol. 45,
Issue. 5,
p.
743.
Leung, A.Y.T.
Zhou, Zhenhuan
and
Xu, Xinsheng
2014.
Determination of stress intensity factors by the finite element discretized symplectic method.
International Journal of Solids and Structures,
Vol. 51,
Issue. 5,
p.
1115.
Raghavan, R.S.
Kumar, A.M
and
Narayanrao, R.
2015.
Intercalation induced surface cracking in electrode particles.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 95,
Issue. 8,
p.
845.
Chen, Bingbing
Zhou, Jianqiu
and
Cai, Rui
2016.
Analytical model for crack propagation in spherical nano electrodes of lithium-ion batteries.
Electrochimica Acta,
Vol. 210,
Issue. ,
p.
7.
Hu, Xiaopeng
Zhao, Yanjie
Cai, Rui
and
Zhou, Jianqiu
2017.
Surface effected fracture behavior of nano-spherical electrodes during lithiation reaction.
Materials Science and Engineering: A,
Vol. 707,
Issue. ,
p.
92.
Wu, X.R.
and
Tong, D.H.
2018.
Evaluation of various analytical weight function methods base on exact K-solutions of an edge-cracked circular disc.
Engineering Fracture Mechanics,
Vol. 189,
Issue. ,
p.
64.
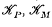 are given exactly by
are given exactly by