Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Falconer, K. J.
1994.
Bounded distortion and dimension for non-conformal repellers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 2,
p.
315.
Pollicott, Mark
and
Weiss, Howard
1994.
The dimensions of some self-affine limit sets in the plane and hyperbolic sets.
Journal of Statistical Physics,
Vol. 77,
Issue. 3-4,
p.
841.
Hueter, Irene
and
Lalley, Steven P.
1995.
Falconer's formula for the Hausdorff dimension of a self-affine set in R2.
Ergodic Theory and Dynamical Systems,
Vol. 15,
Issue. 1,
p.
77.
Kenyon, R.
and
Peres, Y.
1996.
Hausdorff dimensions of sofic affine-invariant sets.
Israel Journal of Mathematics,
Vol. 94,
Issue. 1,
p.
157.
Kenyon, R.
and
Peres, Y.
1996.
Measures of full dimension on affine-invariant sets.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 2,
p.
307.
Edalat, Abbas
1997.
Domains for Computation in Mathematics, Physics and Exact Real Arithmetic.
Bulletin of Symbolic Logic,
Vol. 3,
Issue. 4,
p.
401.
Chin, Wai
Hunt, Brian
and
Yorke, James
1997.
Correlation dimension for iterated function systems.
Transactions of the American Mathematical Society,
Vol. 349,
Issue. 5,
p.
1783.
Olsen, L.
1998.
Self-affine multifractal Sierpinski sponges in ℝd.
Pacific Journal of Mathematics,
Vol. 183,
Issue. 1,
p.
143.
Falconer, Kenneth J.
and
Lammering, Birger
1998.
Fractal Properties of Generalized Sierpiński Triangles.
Fractals,
Vol. 06,
Issue. 01,
p.
31.
Dihe, Hu
1998.
The classification of statistically recursive sets.
Wuhan University Journal of Natural Sciences,
Vol. 3,
Issue. 3,
p.
270.
Edalat, Abbas
and
Parry, Joseph
1998.
An Algorithm to Estimate the Hausdorff Dimension of Self-Affine Sets.
Electronic Notes in Theoretical Computer Science,
Vol. 13,
Issue. ,
p.
31.
Dihe, Hu
1998.
The construction of statistically recursive sets.
Wuhan University Journal of Natural Sciences,
Vol. 3,
Issue. 3,
p.
265.
Falconer, K J
1999.
Generalized dimensions of measures on self-affine sets.
Nonlinearity,
Vol. 12,
Issue. 4,
p.
877.
Schmid, P.E.
1999.
Advances in Ecological Research Volume 30.
Vol. 30,
Issue. ,
p.
339.
Peres, Yuval
and
Solomyak, Boris
2000.
Fractal Geometry and Stochastics II.
p.
95.
Teufl, Elmar
2003.
Fractals in Graz 2001.
p.
263.
Su, Hua
2003.
Dimensions of Self-Affine Sets with Overlaps.
Chinese Annals of Mathematics,
Vol. 24,
Issue. 03,
p.
275.
PALAGALLO, JUDITH
and
PALMER, MATTHEW
2004.
ANALYSIS OF AN IRREGULAR SIERPINSKI TRIANGLE.
Fractals,
Vol. 12,
Issue. 01,
p.
137.
Yu, Jinghu
and
Ding, Lixin
2004.
HAUSDORFF DIMENSION OF GENERALIZED STATISTICALLY SELF-AFFINE FRACTALS.
Acta Mathematica Scientia,
Vol. 24,
Issue. 3,
p.
421.
Allaart, Pieter C.
and
Kawamura, Kiko
2007.
Dimensions of the coordinate functions of space-filling curves.
Journal of Mathematical Analysis and Applications,
Vol. 335,
Issue. 2,
p.
1161.
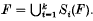 . We obtain estimates for the Hausdorff and box-counting dimensions of such sets, and in particular derive an exact expression for the box-counting dimension in certain cases. These estimates are given in terms of the singular value functions of affine transformations associated with the Si. This paper is a sequel to 4, which presented a formula for the dimensions that was valid in almost all cases.
. We obtain estimates for the Hausdorff and box-counting dimensions of such sets, and in particular derive an exact expression for the box-counting dimension in certain cases. These estimates are given in terms of the singular value functions of affine transformations associated with the Si. This paper is a sequel to 4, which presented a formula for the dimensions that was valid in almost all cases.