Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T07:47:56.544Z Has data issue: false hasContentIssue false
  • English
  • Français

The determination of thermal stresses in dissimilar media

Published online by Cambridge University Press:  24 October 2008

K. Aderogba
K. Aderogba
Affiliation:
University of Lagos, Nigeria
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that if, in an infinite homogeneous unbounded elastic heat-conducting solid, we are given the thermal stresses 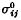which arise when any arbitrarily shaped subregion of the upper half-space z > 0 is emitting any quantity of heat into the surrounding, then on introducing a different heat-conducting material into the half-space z < 0, the new thermal stresses 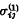in z >0 and 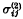in z < 0 are explicitly expressible in an invariant form in terms of the known thermal stresses 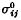in the homogeneous infinite solid. Specialization of the derived dependence shows that the physically interesting interfacial discontinuities inherent in the problem admit the representation

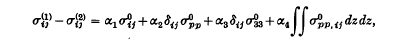
while the traction transmitted across the interface takes the form

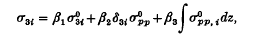
where αi and βi are constants. An application is then made to the case when the region emitting heat into the surrounding is ellipsoidal, since this is a fundamental shape of practical importance. Applications can however be made to any shape of the region emitting heat, provided that the corresponding harmonic and biharmonic potentials are available.

The paper may be considered to have its origin in the half-space theorem of Lorentz in hydrodynamics.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 3 , May 1981 , pp. 533 - 542
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Butler, S. E. J.Proc. Cambridge Philos. Soc. 49 (1953), 169–174.CrossRefGoogle Scholar
(2)Dyson, F. W.Q. J. Pure and Appl. Math. 25 (1891), 259–288.Google Scholar
(3)Eshelby, J. D.Proc. Roy. Soc. Lond. A 252 (1959), 561–569.Google Scholar
(4)Ferrers, N. M.Q. J. Pure and Appl. Math. 14 (1877), 1–22.Google Scholar
(5)Goodier, J. N.Philosophical Magazine 23 (1937), 1017–1032.Google Scholar
(6)Green, A. E. and Zerna, W.Theoretical Elasticity (Oxford University Press 1968).Google Scholar
(7)Guell, D. L. and Dundurs, J.Bevel. Theor. Appl. Mech. 3 (1967), 199–211.Google Scholar
(8)Happel, J. and Brenner, H.Low Reynolds Number Hydrodynamics (Noordhoff International Publishers, 1973).Google Scholar
(9)Hili, R.Continuum Mechanics and Related Problems of Analysis (Moscow, 1972, 597–604).Google Scholar
(10)Milne-Thomson, L. M.Proc. Cambridge Philos. Soc. 36 (1940), 246–248.CrossRefGoogle Scholar
(11)Mindlin, R. D. and Cheng, D. H.J. Appl. Phys. 21 (1950), 931–933.CrossRefGoogle Scholar
(12)Min'dlin, R. D.Proc. Midwestern Conf. Sol. Mech. 1 (1953), 56–59.Google Scholar
(13)Packham, B. A. and Shail, R.Proc. Cambridge Philos. Soc. 69 (1971), 443–448.CrossRefGoogle Scholar
(14)Packham, B. A. and Shail, R.. J. of Elasticity 8 (1978), 393–407.CrossRefGoogle Scholar
(15)Seo, K. and Mura, T.J. Appl. Mech. 46 (1979), 568–572.CrossRefGoogle Scholar
(16)Weiss, P.Proc. Cambridge Philos. Soc. 40 (1944), 259–261.CrossRefGoogle Scholar