No CrossRef data available.
The definition of measure in function space
Published online by Cambridge University Press: 24 October 2008
Extract
A fundamental result in the theory of measure in the space Ω of real functions x(t) of a real variable t is the following theorem of Kolmogoroff:
Theorem 1. Suppose that functions F(t1, …, tn; b1 …, bn) = F(t; b) are defined for positive integers n and real numbers t1, …, tn, b1, …, bn, and have the following properties:
(1·1) For every fixedt1, …, tn, F(t; b) has non-negative differences
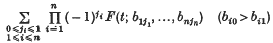
with respect to the variables bl, b2,…, bn, and is continuous on the right with respect to each of them;
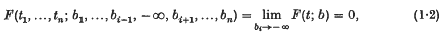
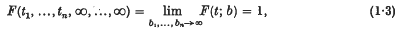
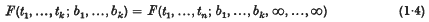
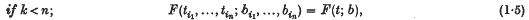
if (i1, …, in) is any permutation of (1, 2, …, n). Then a measure P(X) can be defined in a Borel system of subsets of Ω in such a way that the set of functions satisfying
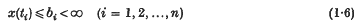
is measurable for any realbi, tiand has measure F(t; b).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 1 , January 1950 , pp. 19 - 27
- Copyright
- Copyright © Cambridge Philosophical Society 1950


