Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T11:28:21.108Z Has data issue: false hasContentIssue false
  • English
  • Français

The core model for sequences of measures. I

Published online by Cambridge University Press:  24 October 2008

William J. Mitchell
William J. Mitchell
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, PA 16802, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

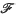The model K() presented in this paper is a new inner model of ZFC which can contain measurable cardinals of high order. Like the model L(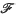) of [14], from which it is derived, K(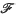) is constructed from a sequence 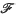of filters such that K(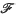) satisfies for each (α, β) ε domain (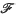) that 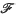(α,β) is a measure of order β on α and the only measures in K(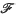) are the measures 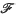(α,β). Furthermore K(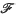), like L(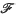), has many of the basic properties of L: the GCH and ⃟ hold and there is a definable well ordering which is 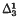on the reals. The model K(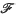) is derived from L(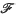) by using techniques of Dodd and Jensen [2–5] to build in absoluteness for measurability and related properties.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 2 , March 1984 , pp. 229 - 260
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bull, E. L. Jr. Successive large cardinals. Ann. Math. Logic 15 (1978), 161–191.CrossRefGoogle Scholar
[2]Dodd, A. J.. The Core Model. L.M.S. Lecture Notes series no. 61 (Cambridge University Press, 1982).CrossRefGoogle Scholar
[3]Dodd, A. J. and Jensen, R.. The core model. Ann. Math. Logic 20 (1981), 43–75.CrossRefGoogle Scholar
[4]Dodd, A. J. and Jensen, R.. The covering lemma for K. Ann. Math. Logic 22 (1982) 1–30.CrossRefGoogle Scholar
[5]Dodd, A. J. and Jensen, R.. The covering lemma for L(U). Ann. Math. Logic 22 (1982), 127–135.CrossRefGoogle Scholar
[6]Jech, T.. Set Theory. (Academic Press 1978.)Google Scholar
[7]Jensen, R.. The fine structure of the constructible hierarchy. Ann. Math. Logic 4 (1972), 229–309.CrossRefGoogle Scholar
[8]Kanamori, A.. Ultrafilters over a measurable cardinal. Ann. Math. Logic 11 (1976), 315–356.CrossRefGoogle Scholar
[9]Kanamori, A. and Magidor, M.. The evolution of large cardinals in set theory. In Higher Set Theory, Lecture Notes in Math. vol. 699 (Springer-Verlag, 1978), 99–275.CrossRefGoogle Scholar
[10]Kunen, K.. Some applications of iterated ultrapowers in set theory. Ann. Math. Logic 1 (1970), 179–227.CrossRefGoogle Scholar
[11]Kunen, K.. Saturated ideals. J. Symbolic Logic 43 (1978), 65–76.CrossRefGoogle Scholar
[12]Magidor, M.. On the singular cardinals problem, II. Ann. of Math. 106 (1977), 517–547.CrossRefGoogle Scholar
[13]Magidor, M.. Changing cofinality of cardinals. Fund. Math. 99 (1978), 61–71.CrossRefGoogle Scholar
[14]Mitchell, W. J.. Sets constructible from sequences of ultrafilters. J. Symbolic Logic 39 (1974), 57–66.CrossRefGoogle Scholar
[15]Mitchell, W. J.. Indiscernibles, skies and ideals. In Proceedings of the 1983 Boulder Summer Conference in Set Theory. Contemporary Mathematics (American Mathematical Society, in the Press).Google Scholar
[16]Mitchell, W. J.. How weak is a closed unbounded ultrafilter? In Logic Colloquium 1980, Studies in Logic vol. 108 (North-Holland, 1982), 209–230.Google Scholar
[17]Silver, J.. On the singular cardinals problem. In Proc. Internat. Congr. Math., Vancouver 1974, vol. 1, pp. 265–268.Google Scholar
[18]Solovay, R. M., Reinhart, W. N. and Kanamori, A.. Strong axioms of infinity and elementary embeddings. Ann. Math. Logic 13 (1978), 73–116.CrossRefGoogle Scholar
[19]Woodin, H.. Hypermeasures and the closed, unbounded filter. (In the Press.)Google Scholar
[20]Woodin, H.. Private communication.Google Scholar