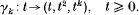Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Choi, Youngwoo
2003.
The Lp-Lp mapping properties of convolution operators with the affine arclength measure on space curves.
Journal of the Australian Mathematical Society,
Vol. 75,
Issue. 2,
p.
247.
Dendrinos, Spyridon
Laghi, Norberto
and
Wright, James
2009.
Universal Lp improving for averages along polynomial curves in low dimensions.
Journal of Functional Analysis,
Vol. 257,
Issue. 5,
p.
1355.
Choi, Youngwoo
2011.
Convolution estimates related to space curves.
Journal of Inequalities and Applications,
Vol. 2011,
Issue. 1,