Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T10:43:58.194Z Has data issue: false hasContentIssue false
  • English
  • Français

Convex curves in which a triangle can revolve

Published online by Cambridge University Press:  24 October 2008

H. T. Croft
H. T. Croft
Affiliation:
Peterhouse, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

We shall be considering plane closed convex curves Γ (whose interior plus boundary will be denoted by Σ ≡ Σ(Γ)) in which we can inscribe a large set (in various senses to be made precise) of equilateral triangles or e-triangles for short; and in particular an e-triangle of side-length 1 is called an E-triangle or just an E. More formally we define the sets 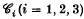to be the sets of closed convex Γ for which, respectively:

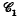: each point of Γ is the vertex of some inscribed E;

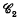: Γ contains the vertices of some E in each orientation in the plane;

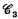: an E can be moved round continuously, through angle 2π, with all vertices on Γ throughout.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 3 , November 1980 , pp. 385 - 393
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Fischer, H. J.Kurven, in denen ein Drei- oder Vieleck so herumgeführt werden kann, dass seine Ecken die Kurve durchlaufen. Deutsche Math. 1 (1936), 485–498.Google Scholar
(2)Hadwiger, H.Ungelöste Probleme 21. Elem. Math. 13 (1958), 13–14Google Scholar
Nachtragen, 13 (1958), 59–60, 86.Google Scholar
(3)Lumer, G.Poligonos inscriptibles en curvas convexas, Rev. Un. Math. Argentina 17 (1955), 97–102 (1956).Google Scholar
(4)Croft, H. T.Some geometrical thoughts. Math. Gaz. 49 (1965), 45–49.CrossRefGoogle Scholar
(5)Yaglom, I. M. and Boltyanskii, V. G.Convex Figures. New York, Holt, Rinehart and Winston, 1961).Google Scholar
(6)Schneider, R.Gleikörper in konvexen Polytopen. J. reine angew. Math. 248 (1971), 193–220.Google Scholar