No CrossRef data available.
The convergence of polynomial expansions of positive harmonic functions
Published online by Cambridge University Press: 24 October 2008
Extract
Let B(r) denote the open ball of radius r centred at the origin 0 of the Euclidean space ℝN, where N ≥ 2. It is well known that if h is harmonic in B(1), then there exist homogeneous harmonic polynomials Hj of degree j in ℝN such that 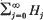 converges absolutely and locally uniformly to h in B(1) (see, e.g. Brelot[1], Appendice). Further, this series is unique and each Hj is the sum of all the monomial terms of degree j in the multiple Taylor series of h centred at 0. We call
converges absolutely and locally uniformly to h in B(1) (see, e.g. Brelot[1], Appendice). Further, this series is unique and each Hj is the sum of all the monomial terms of degree j in the multiple Taylor series of h centred at 0. We call 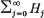 the polynomial expansion of h.
the polynomial expansion of h.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 117 , Issue 1 , January 1995 , pp. 165 - 174
- Copyright
- Copyright © Cambridge Philosophical Society 1995


