No CrossRef data available.
The convergence of a sum of independent random variables
Published online by Cambridge University Press: 24 October 2008
Extract
Let Xν, ν= l, 2, …, n be n independent random variables in k-dimensional (real) Euclidean space Rk, which have, for each ν, finite fourth moments β4ii = l,…, k. In the case when the Xν are identically distributed, have zero means, and unit covariance matrices, Esseen(1) has discussed the rate of convergence of the distribution of the sums

If 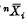 denotes the projection of
denotes the projection of 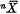 on the ith coordinate axis, Esseen proves that if
on the ith coordinate axis, Esseen proves that if
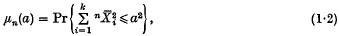
and ψ(a) denotes the corresponding normal (radial) distribution function of the same first and second moments as μn(a), then

where 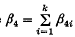 and C is a constant depending only on k. (C, without a subscript, will denote everywhere a constant depending only on k.)
and C is a constant depending only on k. (C, without a subscript, will denote everywhere a constant depending only on k.)
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 2 , April 1963 , pp. 411 - 416
- Copyright
- Copyright © Cambridge Philosophical Society 1963


