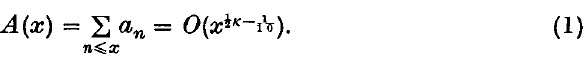Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guinand, A. P.
1947.
Integral modular forms and summation formulae.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 43,
Issue. 1,
p.
127.
Pennington, W. B.
1951.
On the order of magnitude of Ramanujan's arithmetical function τ(n).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 47,
Issue. 4,
p.
668.
Apostol, T. M.
and
Sklar, Abe
1957.
The approximate functional equation of Hecke’s Dirichlet series.
Transactions of the American Mathematical Society,
Vol. 86,
Issue. 2,
p.
446.
Berndt, Bruce C.
1969.
Arithmetical identities and Hecke's functional equation.
Proceedings of the Edinburgh Mathematical Society,
Vol. 16,
Issue. 3,
p.
221.
Moreno, Carlos Julio
1972.
Prime number theorems for the coefficients of modular forms.
Bulletin of the American Mathematical Society,
Vol. 78,
Issue. 5,
p.
796.
Parson, L. A.
and
Sheingorn, Mark
1981.
Analytic Number Theory.
Vol. 899,
Issue. ,
p.
422.
Maass, H.
1983.
Lectures on Modular Functions of One Complex Variable.
p.
109.
Ferguson, H. R. P.
Major, R. D.
Powell, K. E.
and
Throolin, H. G.
1984.
On zeros of Mellin transforms of 𝑆𝐿₂(𝑍) cusp forms.
Mathematics of Computation,
Vol. 42,
Issue. 165,
p.
241.
Rankin, R. A.
1986.
Fourier coefficients of cusp forms.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 100,
Issue. 1,
p.
5.
Berndt, Bruce C.
Kohnen, Winfried
and
Ono, Ken
2003.
Number Theory and Modular Forms.
Vol. 10,
Issue. ,
p.
9.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
13.
Blomer, Valentin
and
Brumley, Farrell
2013.
The role of the Ramanujan conjecture in analytic number theory.
Bulletin of the American Mathematical Society,
Vol. 50,
Issue. 2,
p.
267.
Goldfeld, Dorian
and
Sengupta, Jyoti
2016.
First moments of Fourier coefficients of GL(r) cusp forms.
Journal of Number Theory,
Vol. 161,
Issue. ,
p.
435.
Elliott, P. D. T. A.
2017.
Analytic Number Theory, Modular Forms and q-Hypergeometric Series.
Vol. 221,
Issue. ,
p.
267.
Pal, Sridip
2020.
Bound on asymptotics of magnitude of three point coefficients in 2D CFT.
Journal of High Energy Physics,
Vol. 2020,
Issue. 1,
Wyman, Emmett L.
Xi, Yakun
and
Zelditch, Steve
2023.
Fourier coefficients of restrictions of eigenfunctions.
Science China Mathematics,
Vol. 66,
Issue. 8,
p.
1849.
Hou, Yanjie
Yan, Xiaofei
and
Zhang, Deyu
2023.
ON HIGHER MOMENTS OF HECKE EIGENVALUES FOR THE CONGRUENCE GROUP.
Rocky Mountain Journal of Mathematics,
Vol. 53,
Issue. 6,
Goldfeld, Dorian
Hinkle, Gerhardt
and
Hoffstein, Jeffrey
2024.
The shifted convolution L-function for Maass forms.
Research in Number Theory,
Vol. 10,
Issue. 4,


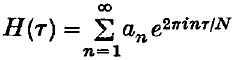 is an integral modular form of dimensions − κ, where κ > 0, and
is an integral modular form of dimensions − κ, where κ > 0, and 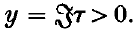 The purpose of this note is to prove that
The purpose of this note is to prove that